Void Space

发表于 更新于 分类于

倍增算法

关联复习-树链剖分

树链剖分的应用场景？ （树的路径操作、子树的操作）

LCA（Least Common Ancestors），即最近公共祖先。 是指这样一个问题：在有根树中，找出某两个结点u和v最近的公共祖先（另一种说法，离树根最远的公共祖先）。

RMQ

关于RMQ问题

RMQ（Range Minimum/Maximum Query），即区间最值查询。是指这样一个问题：对于长度为n的数列A，回答若干询问RMQ（A,i,j）(i,j<=n)，返回数列A中指定区间[i，j]中的最大/小值。

LCA问题和RMQ问题的关系？

LCA《-》RMQ可以互相转换

阅读全文 »

发表于 更新于 分类于

树链剖分 轻重链剖分

树链剖分即轻重链剖分，两者是一个概念

轻重链剖分

树链剖分 - 轻重链剖分

  • 将树剖成一条条不相交的从祖先到子孙的链。

  • 设\(\text{size}[x]\)表示\(x\)点的子树大小， \(\text{size}[x] = 1 + \text{sum}(\text{size}[y])\)，其中\(y\)是\(x\)的儿子。

  • 对于每个点\(x\)，将儿子中\(\text{size}\)最大的那个儿子作为它的重儿子，剩下的作为轻儿子。

    阅读全文 »

发表于 更新于 分类于

2-SAT

SAT 问题定义

SAT的全称：satisfiability（可满足性）

有一个由N个布尔值组成的序列A，给出一些限制关系，比如A[x] AND A[y]=0、A[x] OR A[y] OR A[z]=1等，要确定A[0..N-1]的值，使得其满足所有限制关系，这就是SAT问题。

2-SAT 特殊点

特别的，若每种限制关系中最多只对两个元素进行限制，则称为2-SAT问题。

2-SAT问题是有多项式解法的，而3-SAT就是npc问题。

阅读全文 »

发表于 更新于 分类于

强连通分量

例题一

  • 给定一个有向图，统计有多少点对u, v(u<v)满足： u可以到达v，且v可以到达u。

  • 思考：如何解决？

  • 暴力？复杂度不可想象…

强连通分量定义

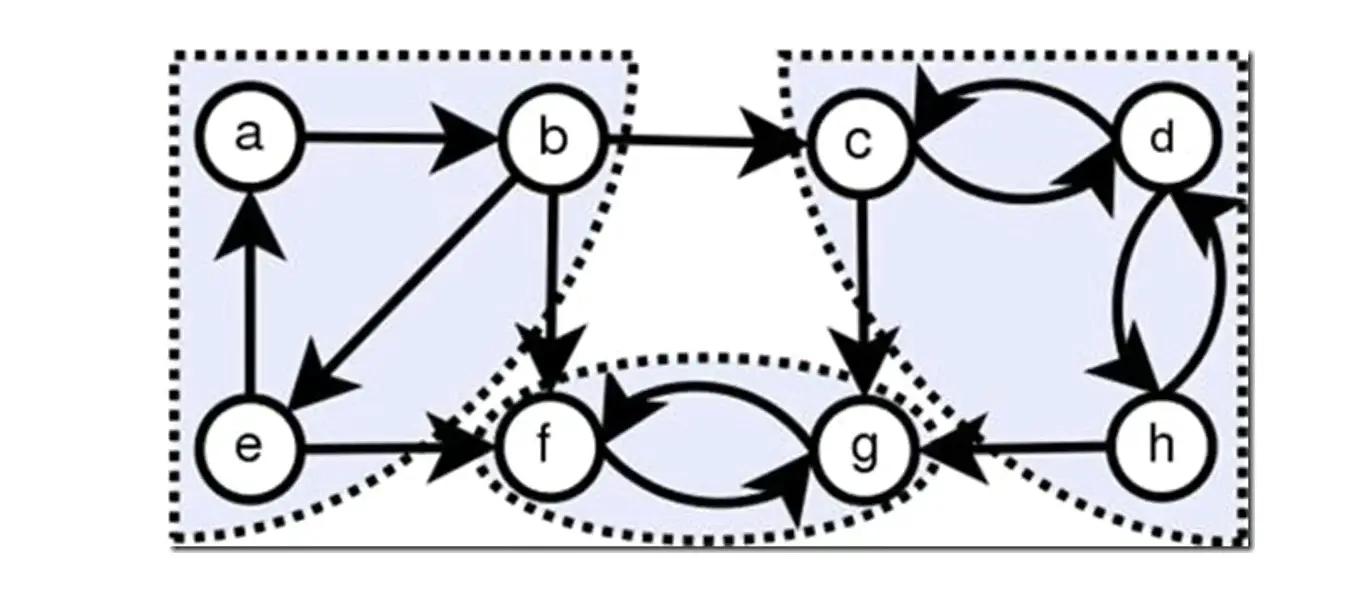
在一个有向图中，选取一个点集S，如果对于S中的任意两点u, v都满足u可以到达v，则称S是强连通的。

如果一个强连通点集S中，不能再加入更多的点使得它仍然强连通，则称S是强连通分量。

阅读全文 »

发表于 更新于 分类于

区间 DP

DP回顾

DP三个特征（基本条件）：

  • 重叠子问题
  • 最优子结构
  • 无后效性

重叠子问题：就是影响到前面的
最优子结构：局部是最优的，北京到上海是北京到杭州的子结构
无后效性：大不影响小

思考：DP和搜索的区别？

引导题目

阅读全文 »

发表于 更新于 分类于

Sublime 默认新文件为 cpp

import sublime, sublime_plugin

class EverythingIsPowerShell(sublime_plugin.EventListener):
    def on_new(self, view):
        view.set_syntax_file('Packages/C++/C++.sublime-syntax')

创建一个py文件，放到package/user中即可

发表于 更新于 分类于

KMP 字符串匹配

kmp举例

  • 给定字符串A和字符串B，请判断B是否是A的子串（即：A串是否包含B串）
  • 比如，字符串A=“Dingba hen shuai!” 字符串B=“shuai”
  • A串（等待匹配的串），称为主串（母串）
  • B串（用来匹配的串），称为模式串
阅读全文 »
0%