区间 DP

发表于 更新于 分类于

区间 DP

DP回顾

DP三个特征（基本条件）：

  • 重叠子问题
  • 最优子结构
  • 无后效性

重叠子问题：就是影响到前面的
最优子结构：局部是最优的，北京到上海是北京到杭州的子结构
无后效性：大不影响小

思考：DP和搜索的区别？

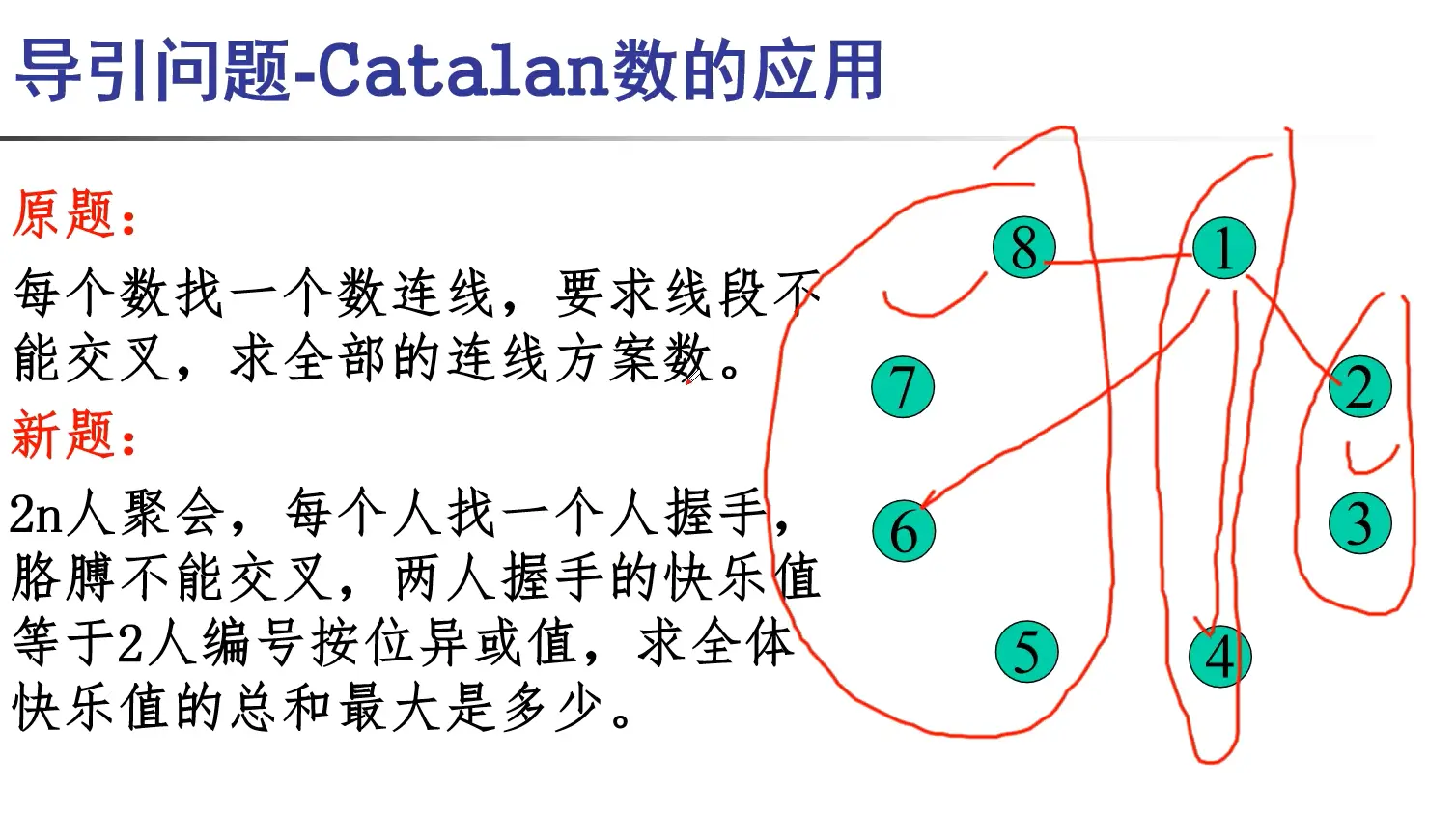
引导题目

连一条线然后启动分离 改编题：

eg1-石子合并问题

问题描述：
有N堆石子排成一排，每堆石子有一定的数量。
现要将N堆石子合并成一堆。合并的过程只能每次将相邻的两堆石子并成一堆，每次合并花费的代价为这两堆石子的和，经过N-1次合并后成为一堆。求总的代价最小值。

题目来源——NOI1995

选中一个位置，左右两侧是互相独立的子问题→可以递推

题目特点分析：

1、求某个区间的最优解（一般是区间\([1, n]\)）；
2、大的区间由包含于它的小区间组成（转移而来）；
3、满足DP的三个基本条件；

状态，阶段，决策（状态转移）

  • 题目分析：
  • 状态
    • 通用状态的定义：\(\text{DP}[i][j]\)的含义？
    • 目标状态的表示：？？？
  • 阶段的划分：区间长度
  • 决策（状态转移）： \(\text{dp}[i][j]=\min(\text{dp}[i][j], \text{dp}[i][k]+\text{dp}[k+1][j]+\text{w}[i][j])\)

i 到 j 需要的体力值

区间DP小结

  • 阶段的划分：区间长度
  • 状态的表示：枚举起点（不同起点，不同状态）
  • 决策的实现：枚举分割点

区间DP的状态设计相对简单，基本大部分问题都是用 dp[i][j] 代表区间 [i,j] 上的最优解。

状态转移一定是从区间长度短的状态到区间长度长的状态；

代码：

递推迭代

区间DP模板-迭代：

for(int len=2;len<=n;len++)     //区间长度
    for(int i=1;i<=n;i++)       //枚举起点
    {   int j=i+len-1;          //计算出区间终点
        if(j>n) break;          //越界结束
        for(int k=i;k<j;k++)   //枚举分割点，构造状态转移方程
        {
            dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+w[i][j]);
        }
    }

记忆化DFS（推荐

区间DP模板-记忆化DFS：

//推荐记忆化DFS的实现方式，更简单，不容易出错

int MINdfs(int l,int r)
{
    int &D = dp[l][r];  //引用D就代表dp[l][r],这个方法可以简化代码
    if(D != inf) return D; //如果已经搜索过就返回这个值，记忆化搜索的重点
    if(l == r)  return D = 0;//如果l==r，无需合并，所以返回0
    for(int i=l;i<r;i++)  //枚举所有可行的区间分割方案
        D = min(D, MINdfs(l,i) + MINdfs(i+1,r)+ sum[r] - sum[l-1]);
    return D;
}

最大值则改为 max，还有初始化用 -1

eg2-猴子交朋友

n只猴子坐成一圈，每只猴子都有交朋友的时间，交友规则是：

  • 每次只能介绍一只猴子和这只猴子的邻居认识（成为朋友）；
  • 如果介绍猴子A和B认识，那么意味着猴子A和B将认识对方的所有朋友，这次交友的总用时是A和B原来交友时间的总和；
  • 每个猴子都认识自己；

求完成交友任务（所有猴子都相互认识）需要的最短时间。

是一个环形石子合并

问题分析

问题的本质？ ——环形石子合并！

即现在有围成一圈的若干堆石子，求合并所需最小代价。

环形问题转化小技巧：

把前n-1堆石子一个个移到第n个后面，那样环就变成了线，即转化成了有2*n-1堆石子的普通石子合并问题。

最后求：\(\boldsymbol{\min(\mathrm{dp}[s][s+n-1]), s \in [1, n]}\)

eg3-狼

有N匹狼站成一排（从左到右编号为1到N），你必须打败所有的狼才能生存。

每匹狼具有一定的基本攻击力a[i]和辅助攻击力b[i]

杀一匹狼消耗的能量 = 狼的基本攻击力a[i]+相邻两匹狼的辅助攻击力b[i-1]+b[i+1]。

求打败所有的狼所需要的最小能量。

特别说明：如果杀死第k个位置的狼，则接下来k-1和k+1位置的狼变为相邻，以此类推。

题目来源——2014ACM/ICPC亚洲区北京站

题目解析

递推公式，解决：

状态定义：

dp[i][j]——表示从第i头狼到第j头狼全部被杀死所需要的最少能量。

目标状态： dp[1][n]

状态转移：

dp[i][j] = min(dp[i][j], dp[i][k-1]+dp[k+1][j] + a[k]+b[i-1] + b[j+1]);

小细节： b[0] = b[n+1] = 0;

即左右两侧只能用到各1次

eg4-焦躁因子

一个有点难度的区间DP：

在《非诚勿扰》节目中，给定n个男生的序列，序列内的每个人都有一个焦躁因子Di，如果第i个人是第k个出场，那么他的焦躁值为Di * (k-1)， 现在，导演可以通过一个栈来调整序列里面人的出场顺序。 求焦躁总值最小可以是多少。

题目来源——2012 ACM/ICPC Asia Regional Tianjin Online

题目解析

分成两个子问题，1在k处释放

关键点——

导演对于男生出场顺序的影响是有限的！ 比如：

  1. 如果，第一个人第k个出场；
  2. 那么，第2 ～ k的人都要在第一个人前面出场；
  3. 同时，第k+1 ～ n的人都要在k以后出场。

大区间问题 划分成了 小区间的问题。

解决，转移方程

定义状态\(dp[i, j]\)表示，对于区间\([i, j]\)在相对于\(i\)为起点情况下，最小焦躁总值。

\(dp[1, n]\)就是所要求的值。

状态转移方程是——

\[dp[i, j] = (k-i) * Di + dp[i+1, k] + dp[k+1, j] + (k+1-i) * (sum[j] - sum[k])\]

更多练习

参考资料和相关题目

多边形剖分、括号匹配、回文串（IOI2000） 石子合并（NOI1995）、能量项链（NOIP2006）

https://mp.weixin.qq.com/s/vw-Wunkm_zoJMPAZygnW2w

https://www.cnblogs.com/kedebug/archive/2012/12/10/2811053.html

https://blog.csdn.net/my_sunshine26/article/details/77141398

总结

区间DP常规思路总结：

  • 1、切割/合并区间 将大区间无脑切割成两个子区间，分别计算两个子区间的最优值，再通过两个子区间的最优值，计算整个大区间的最优值。

  • 2、last原则 永远不去想第一步要干什么，而是想最后一步是要干什么，然后再去枚举最后一步的所有情况，从而缩小区间。

  • 3、添加辅助维 有时候二维的区间无法表示状态，或者无法进行状态转移的时候，我们可以尝试再增加一个纬度，然后再去想状态转移方程。