差分约束

最长路径

新问题：如何求最长路径？

1、Dijkstra按最短路的方法直接去求最长路？ 思考：为何不可以？ 思考：转换成负权求最短路？（Dij算法的软肋）

2、常见方案： Floyd算法求每对节点之间的最长路经 （因为最长路径也满足最优子结构性质，而Floyd算法的实质就是动态规划）

引子

从不等式方程组求解说起

给定n个变量和m个不等式，形如： \(x[i] - x[j] <= a[k]\) (\(0<=i,j<n\)，\(0<=k<m\)，\(a[k]\)已知) 求 \(x[n-1]-x[0]\) 的最大值。

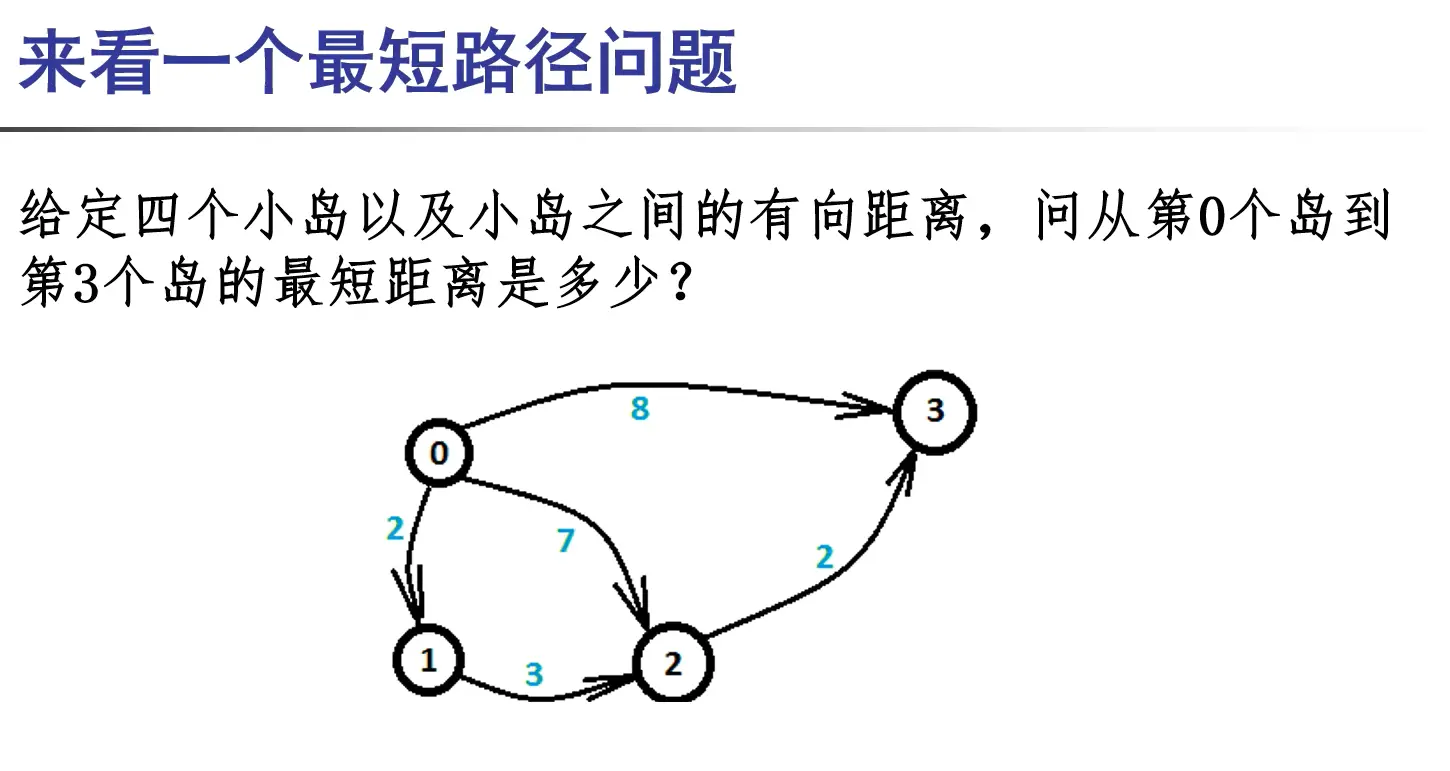
例如：当\(n=4\)，\(m=5\)，不等式组如右，求\(x3-x0\)的最大值。

\(x1 - x0 <= 2\)

\(x2 - x0 <= 7\)

\(x3 - x0 <= 8\)

\(x2 - x1 <= 3\)

\(x3 - x2 <= 2\)

差分约束

关于差分约束系统

• 如果一个系统由n个变量和m个不等式组成，并且这m个不等式均为\(X_i - X_j \leq a[k]\)的形式，这样的系统称为差分约束（difference constraints）系统。

eg-1

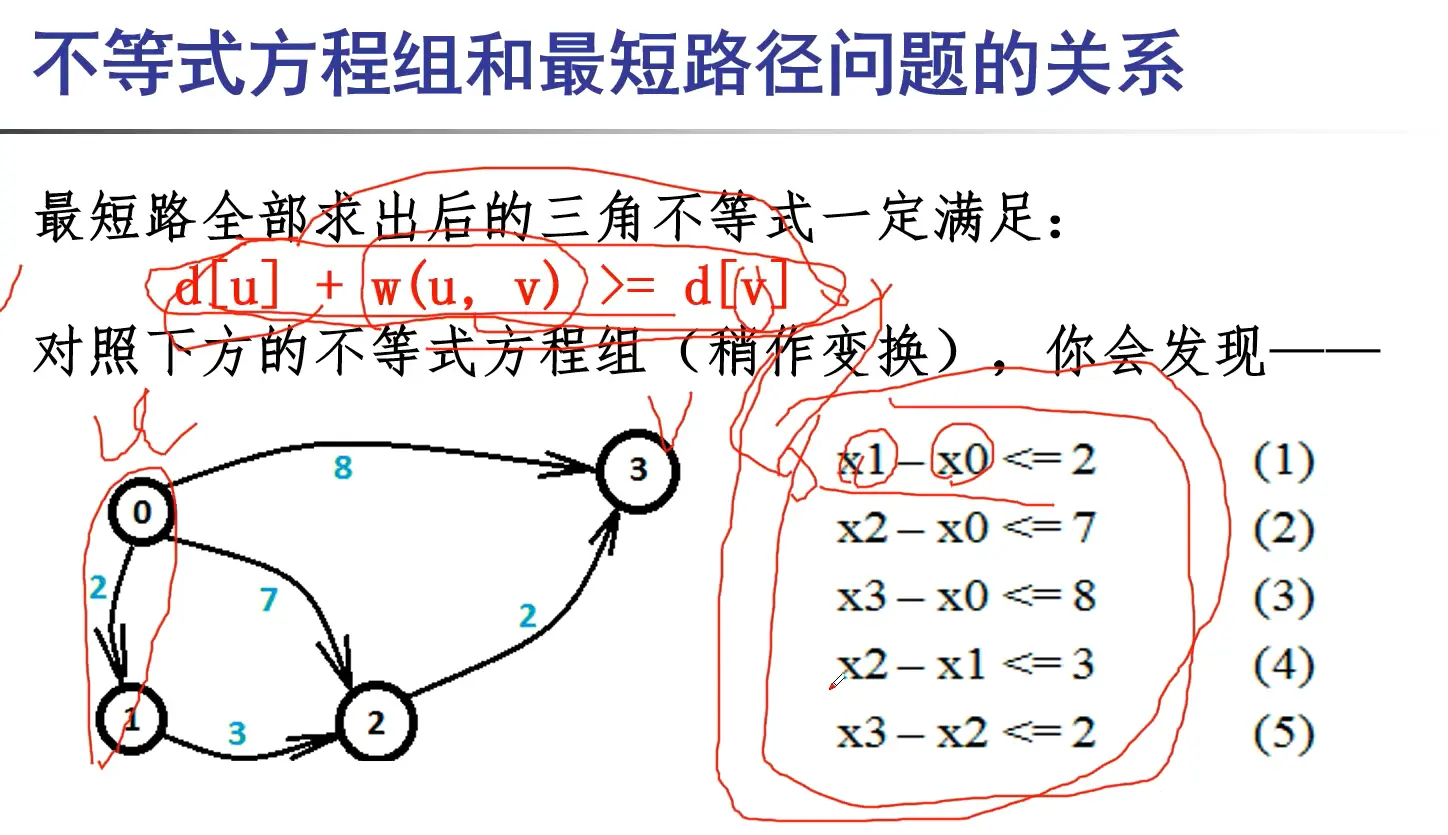
差分约束到最短路，通过松弛的不等式

结论：

差分约束系统可以转换成最短路问题求解！！！

经典的数形结合！！！

通过建立合理的模型，将数学中的不等式关系图形化，用Bellman - ford作为武器，最终解决数学问题！

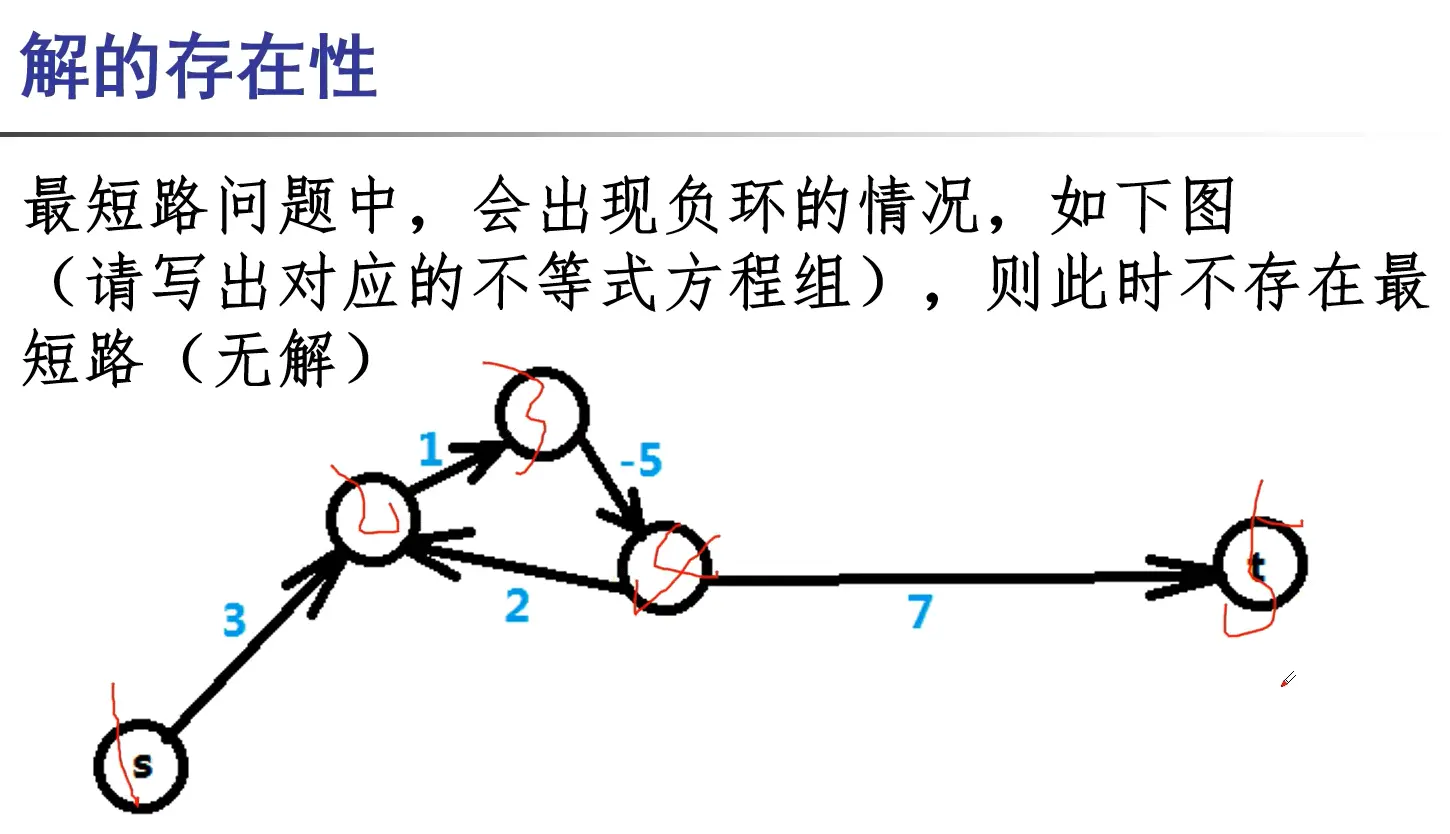
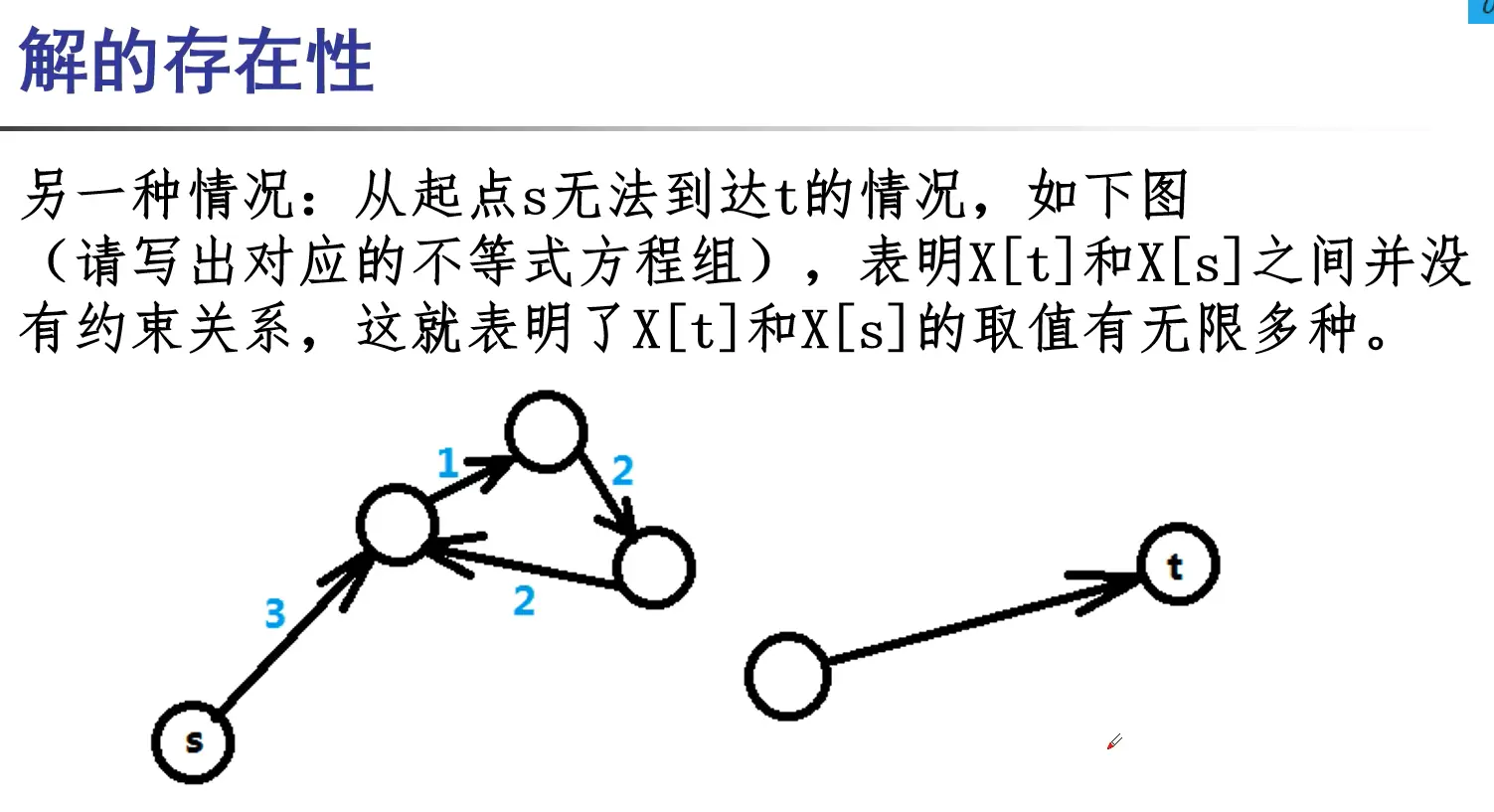
多解 最长路BellmanFord

不等式方程组的标准化

2、如果有形如：\(A - B = c\) 这样的等式呢？ 提示：变换成2个不等式 \(A \!-\! B \geq c\) 和 \(A \!-\! B \leq c\)

3、如果变量都是整数域上的，那么遇到 \(A \!-\! B < c\) 这样的不带等号的不等式，需要将它转化成 \("\leq"\) 或者 \("\geq"\) 的形式，即 \(A \!-\! B \leq c \!-\! 1\)

线性约束

eg-1

差分约束的应用——线性约束

【例1】N个人编号为1-N，并且按照编号顺序排成一条直线，任何两个人的位置不重合，然后给定一些约束条件：

X(X <= 100000)组约束Ax Bx Cx(1 <= Ax < Bx <= N)，表示Ax和Bx的距离不能大于Cx。

Y(Y <= 100000)组约束Ay By Cy(1 <= Ay < By <= N)，表示Ay和By的距离不能小于Cy。

如果这样的排列存在，输出1-N这两个人的最长可能距离，如果不存在，输出-1，如果无限长输出-2。

最短路，即求差分最大值，所有不等式转换为小于等于

令第x个人的位置为\(d[x]\)，则求解目标：

\(d[N] - d[1] <= T\) （最短路）

区间约束

差分约束的应用——区间约束

【例2】给定n（n <= 50000）个整点闭区间和这个区间中至少有多少整点需要被选中，每个区间的范围为[ai, bi]，并且至少有ci个点需要被选中，其中0 <= ai <= bi <= 50000，

求：[0, 50000]至少需要有多少点被选中。

【例2】解题思路：

用\(d[i]\)表示\([0, i]\)这个区间至少有多少点能被选中；

对于每个区间\([a_i, b_i]\)，可以表示成\(d[b_i] - d[a_i - 1] \geq c_i\)；

求解目标：\(d[50000] - d[-1] \geq T\)（最长路）

特别的，隐含条件：\(0 \leq d[i] - d[i-1] \leq 1\)

隐含条件表示整数点

参考资料

• 夜深人静写算法（四）- 最短路和差分约束
• https://blog.csdn.net/whereisherofrom/article/details/78922648