最短路进阶

回顾

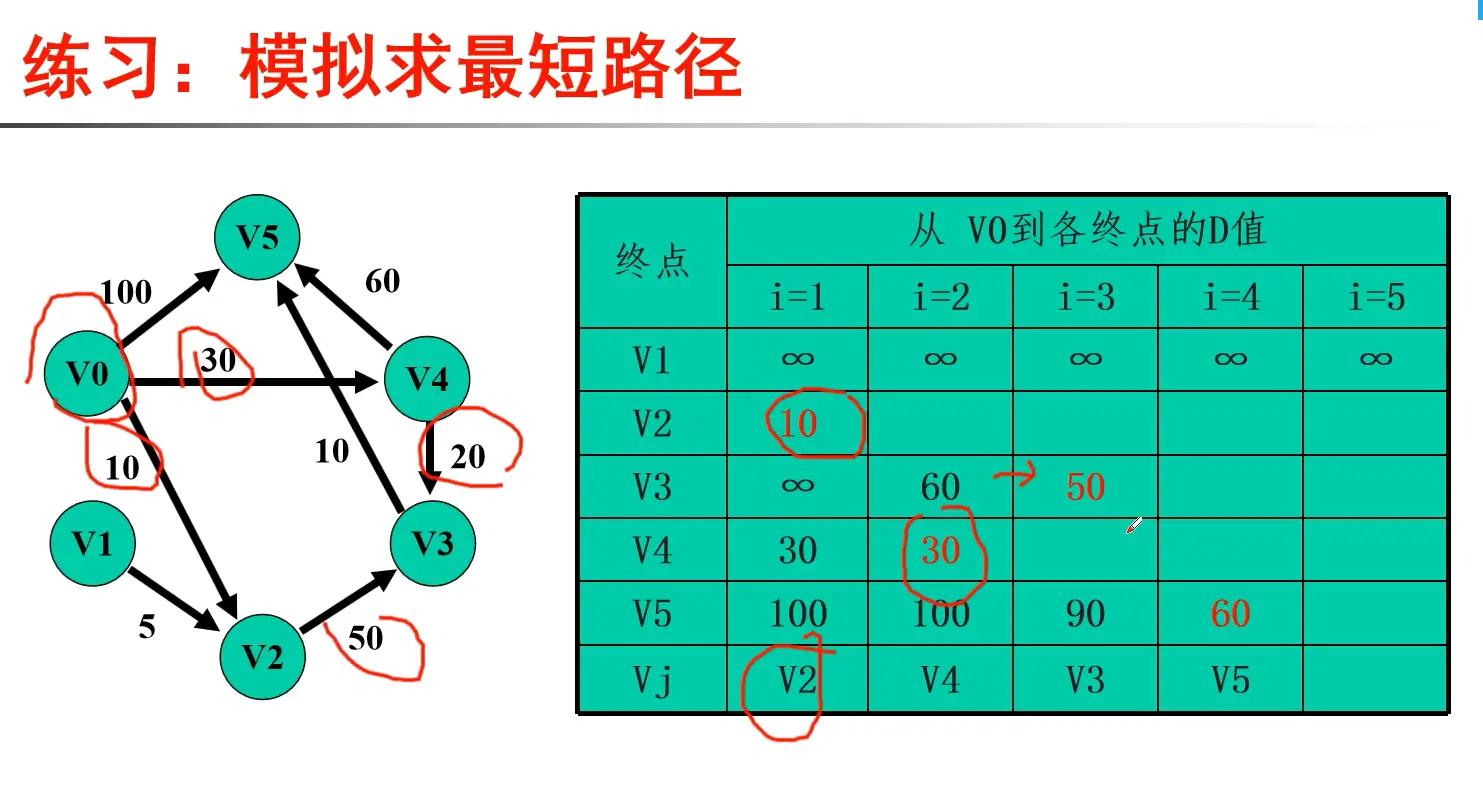
• 按照最短路径的长度递增的次序，依次求得——源点到其余各点的最短路径！
• 先求——最短的那条最短路径（特点？）
• 再求——第二短的最短路径（特点？）
• ……
• 依次类推（特点？）
• ……
• 最终求出所有的最短路径

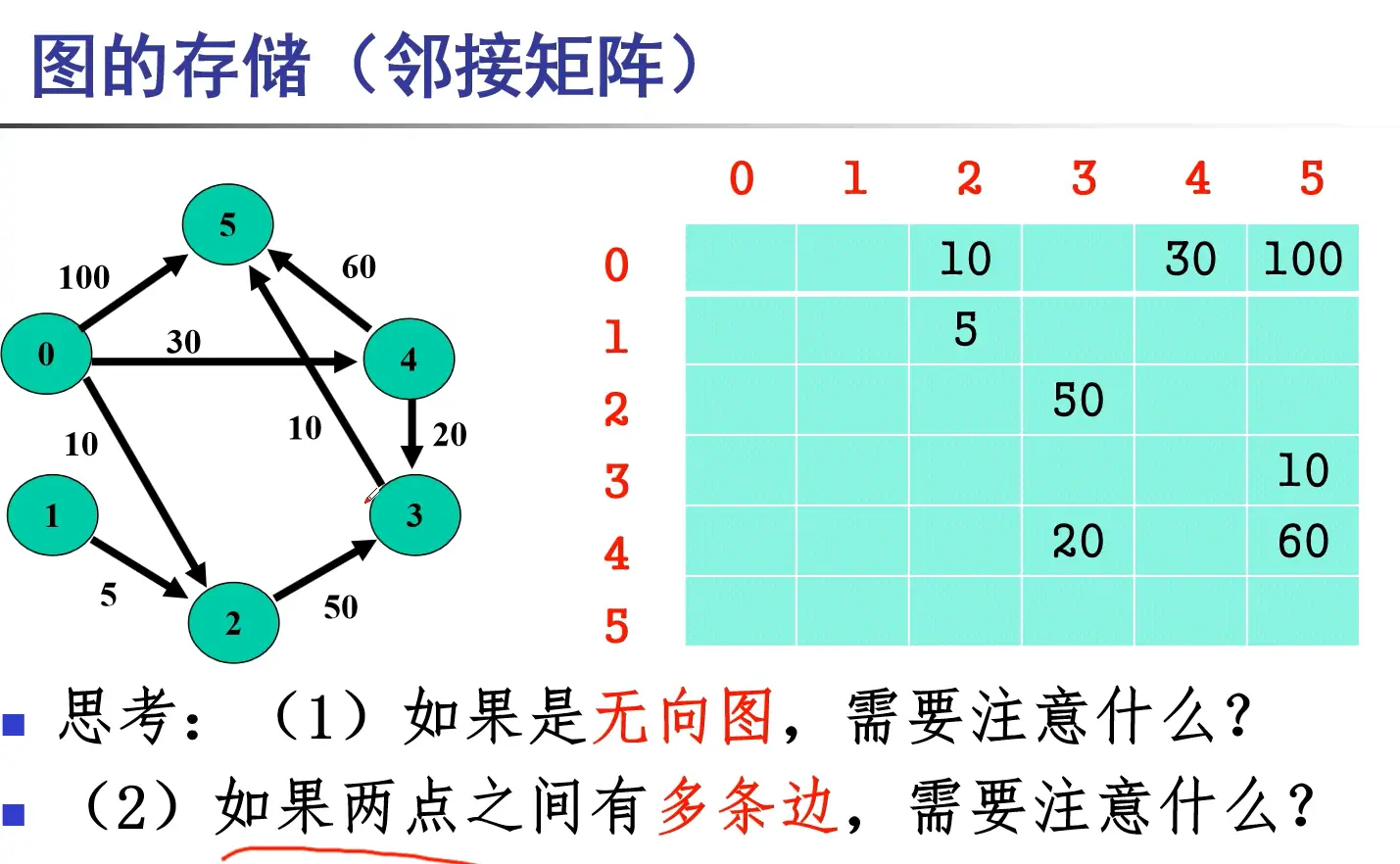
代码

迪杰斯特拉的堆优化

基本思想：

采用邻接表存储图，并利用优先队列维护每个节点的Dist值，避免了每次从n个节点找一个最优解，可以O(1)时间得到本趟的最短路，代价是松弛中的更新操作，每次需要O(LogE)，因为总的松弛操作数和E成正比，所以——

优化后的时间复杂度：ElogE

例题1

1967年，美国著名的社会学家斯坦利·米尔格兰姆提出了一个名为“小世界现象”的著名假说，任何2个素不相识的人中间最多只隔着6个人，即只用6个人就可以将他们联系在一起，因此他的理论也被称为“六度分离”理论。

小胖子对N个人展开了调查，得到了他们之间的相识关系，现在他请你帮忙验证“六度分离”是否成立。

每组输入数据的第一行包含两个整数N,M，分别代表人数（编号1~N），以及关系数。接下来有M行，每行两个整数A,B表示A和B认识。

如果符合“六度分离”理论，输出Yes，否则输出No。

Sample Input
8 7
1 2
2 3
3 4
4 5
5 6
6 7
7 8

Sample Output
Yes

floyd（\(n^3\))

Floyd算法（插点法，经典DP）

• 直接上算法核心代码：

for(k=1;k<=n;k++)      //插入点k在最外层循环很关键！
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            if(dis[i][j] > dis[i][k]+dis[k][j])
                dis[i][j] = dis[i][k]+dis[k][j]

算法思想：从i到j的只经过前k个点的最短路径

算法特点：简单、粗暴、易于实现、可以解决负权

Bellman-Ford

• 直接上算法核心代码（数据存储结构？）：

  for(k=1;k<=n-1;k++)   //n-1个阶段，每个阶段的效果？
      for(i=1;i<=m;i++)//每个阶段，对所有边尝试松弛
          if(dis[v[i]] > dis[u[i]] + w[i])
              dis[v[i]] = dis[u[i]] + w[i]

算法思想：对所有的边进行n-1次松弛操作！

算法复杂度：\(O(nm)\)（比Dijkstra还要慢？） （小优化：不一定需要n-1轮松弛，想想冒泡排序）

算法特点：简洁、可以解决负权负环的情况

增加点数量，点的数量

检测负环：需要Bellman-Ford

Bellman-Ford算法检测负环

• 直接上算法核心代码：

for(k=1;k<=n-1;k++)   //为什么只需要循环n-1次？
    for(i=1;i<=m;i++)
        if(dis[v[i]] > dis[u[i]] + w[i])
            dis[v[i]] = dis[u[i]] + w[i]
flag=0;
for(i=1;i<=m;i++)
    if(dis[v[i]] > dis[u[i]] + w[i]) flag=1;
if(flag==1) ……   //有负权的情况

有负环的情况

SPFA

Bellman-Ford算法的队列优化（SPFA）

基本思想：每次仅对最短路程发生变化了的点的相邻边执行松弛操作。

问题：如何知道当前哪些点的最短路程发生了变化呢？

方案：采用 “队列” 维护

具体操作：先把起点加进队列中，然后松弛和起点相连的所有边，如果松弛成功且该点不在队列中，那么就把这个点入队。然后依次取出队列中的每一个点进行松弛，直到队列为空。

SPFA参考代码：

void spfa(int u) {
    q.push(u);      vis[u] = 1;
    while (!q.empty()) {
        int x = q.front();
        q.pop();    vis[x] = 0;
        for (int i = first[x]; i != -1; i = next[i]) {
            int y = v[i];
            if (dist[x] + w[i] < dist[y]) {
                dist[y] = dist[x] + w[i];
                if (!vis[y]) vis[y] = 1, q.push(y);
            }
        }
    }
}

小结

几种最短路算法的比较分析

Dijkstra，Floyd，Bellman-Ford（SPFA）

时间复杂度？ 负权边的情况？ 判断是否有负权回路？