树链剖分 轻重链剖分

发表于 更新于 分类于

树链剖分 轻重链剖分

树链剖分即轻重链剖分，两者是一个概念

轻重链剖分

树链剖分 - 轻重链剖分

  • 将树剖成一条条不相交的从祖先到子孙的链。

  • 设\(\text{size}[x]\)表示\(x\)点的子树大小， \(\text{size}[x] = 1 + \text{sum}(\text{size}[y])\)，其中\(y\)是\(x\)的儿子。

  • 对于每个点\(x\)，将儿子中\(\text{size}\)最大的那个儿子作为它的重儿子，剩下的作为轻儿子。 ### 树链剖分 - 一些定义

重边：连接x和x重儿子的边。

轻边：连接x和x轻儿子的边。

重链：重边连起来形成的链。每个点恰好属于一条重链。

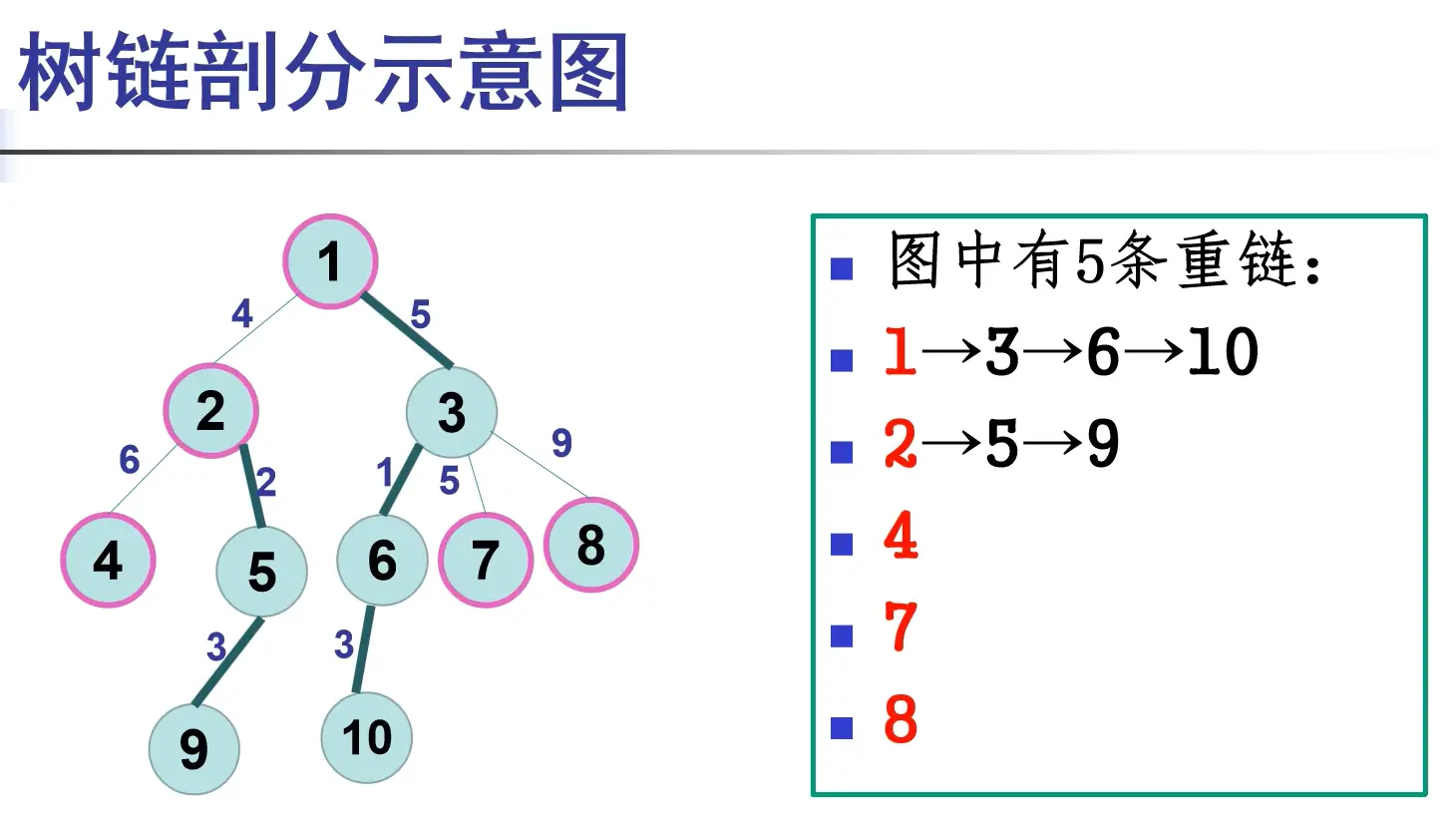
没有子节点的点也算是重链，此外2之后也是新重链

方法

树链剖分

  • 预处理出d[x]表示x的深度；
  • 预处理出f[x]表示x的父亲；
  • 预处理出size[x]表示以x点为根的子树大小；
  • 预处理出son[x]表示x的重儿子；
  • 预处理出top[x]表示x所在重链的顶端。
  • 预处理可以通过两遍DFS在O(n)时间内完成：
  • 第一遍DFS算出size[x], d[x], f[x], 并找到重儿子son[x]。
  • 第二遍DFS算出top[x]，x和x的重儿子的top相同。

代码

第一步：求出树的各种参数

参考代码1(第1次DFS)：

void dfs1(int x, int fath){
    size[x]=1; d[x]=d[fath]+1; //d[0]=0, 根节点深度为1
    son[x] =0; f[x]=fath;   //根节点编号为1，0表示不存在
    for(int i=head[x]; i; i=e[i].nex){
        int to = e[i].to;
        if(to == fath)  continue;
        dfs1(to, x);
        size[x]+=size[to];
        if(size[son[x]]<size[to])  son[x]=to;
    }
}

（1,0）开始调用： 第二步：求出top x

参考代码2(第2次DFS)：

#define N 100005
int head[N],tot,f[N],d[N],son[N],size[N],top[N],n,m;
struct edge{ int to, nex; } e[N<<1];
void dfs2(int x,int topx){
    top[x]=topx;
    if(son[x]!=0) dfs2(son[x],topx);
    for(int i=head[x]; i; i=e[i].nex){
        if(e[i].to !=f[x] && e[i].to !=son[x])
            dfs2(e[i].to, e[i].to);   //开启一个新的重链
    }
}
int main() { ...... dfs1(1, 0); dfs2(1, 1); ...... }

小结

树链剖分小结：

  • 第一遍DFS确定每个节点x的size[x], d[x], f[x], 以及重儿子son[x]。
  • 第二遍DFS确定每个节点x的top[x]，特别指出：x和x的重儿子的top相同。
  • 求top[x]需要用到son[x]、f[x]等信息，所以两个DFS顺序不能颠倒

LCA最近公共祖先

最近公共祖先 - 定义

深度：有根树上x到根的距离。

最近公共祖先lca：u和v的最近公共祖先lca(u,v)定义为u到v路径上深度最小的点。

任何一条路径都能表示成u到lca(u,v)以及v到lca(u,v)这两段深度严格递减的链。

例题：：

  • 给定一棵n个点的树，根节点为1。
  • m次询问两个点的最近公共祖先。
  • \(1 <= n,m <= 100000\)。

代码：

int lca(int x, int y) {
    while (top[x] != top[y]) { // 不在同一条重链
        if (d[top[x]] < d[top[y]]) {
            swap(x, y); // 总是让 top[x] 深度更大
        }
        x = f[top[x]];   // 将 x 往上跳过一条轻边
    }
    // 位于同一条重链的情况
    return d[x] < d[y] ? x : y;
}

时间复杂度

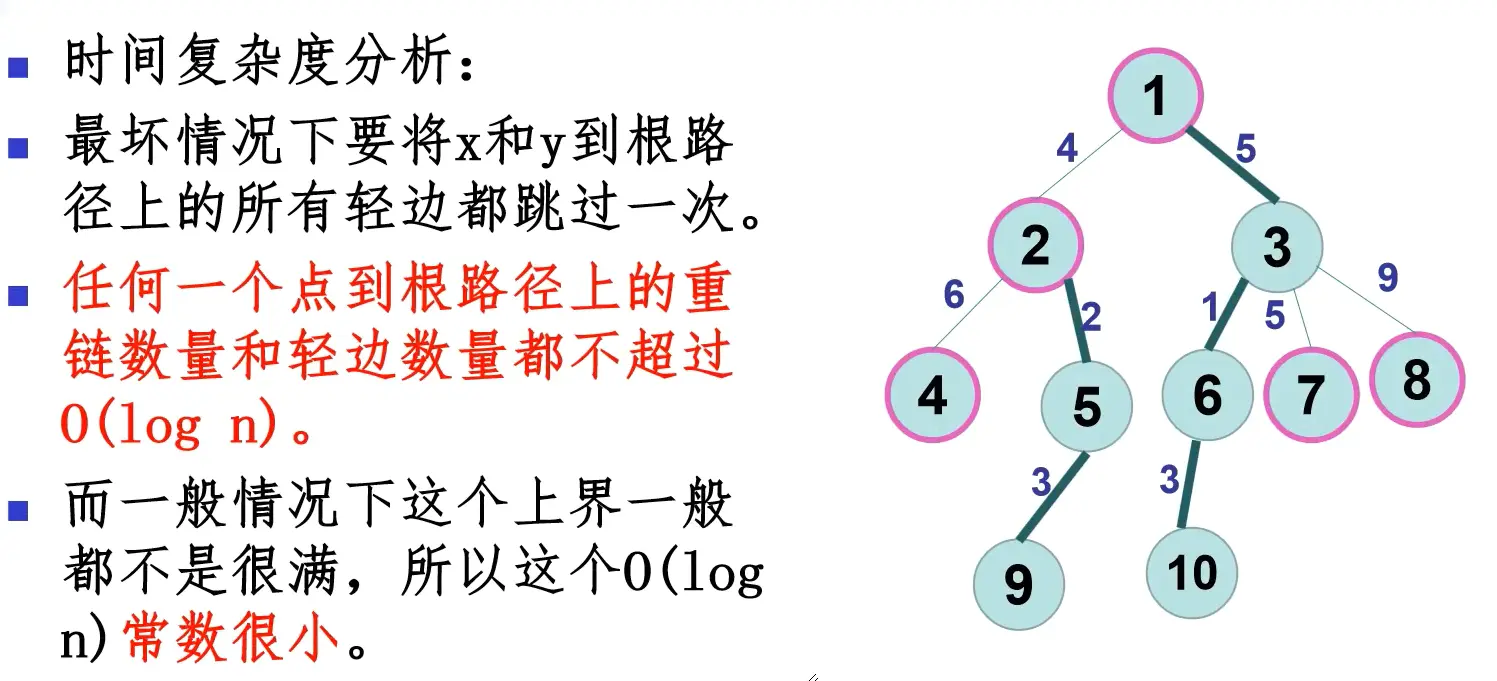
  • 证明？
  • 若y是x的轻儿子，那么存在一个z满足 \(\text{size}[z] \geq \text{size}[y]\)。
  • 又因为 \(\text{size}[z] + \text{size}[y] < \text{size}[x]\)，所以 \(2\text{size}[y] < \text{size}[x]\)。
  • 每次经过一条轻边size至少除以2，所以最多经过 \(O(\log\ n)\) 条轻边。

eg2-树上操作

  • 给定一棵n个点的树，根节点为1，每个点有点权。
  • m次操作，操作有以下四种：
  • 1 x y z 将x到y路径上每个点点权都加上z。
  • 2 x z 将x子树内每个点点权都加上z。
  • 3 x y 查询x到y路径上每个点的点权之和。
  • 4 x 查询x子树内每个点的点权之和。
  • \(1 <= n,m <= 100000\)。

解法：

  • 树链剖分，在第二次DFS中先DFS重儿子再DFS轻儿子；
  • 将依次DFS到的点记录下来，则每条重链是一个连续区间，每个点的子树也是一个连续区间；
  • 对于子树操作，至此转化为了区间操作，可以线段树维护。
  • 对于任意路径操作，要么在同一条重链，要么可以分解成最多log条重链+轻边，同样可以转化为区间操作；
  • 子树操作：\(O(\log n)\)。

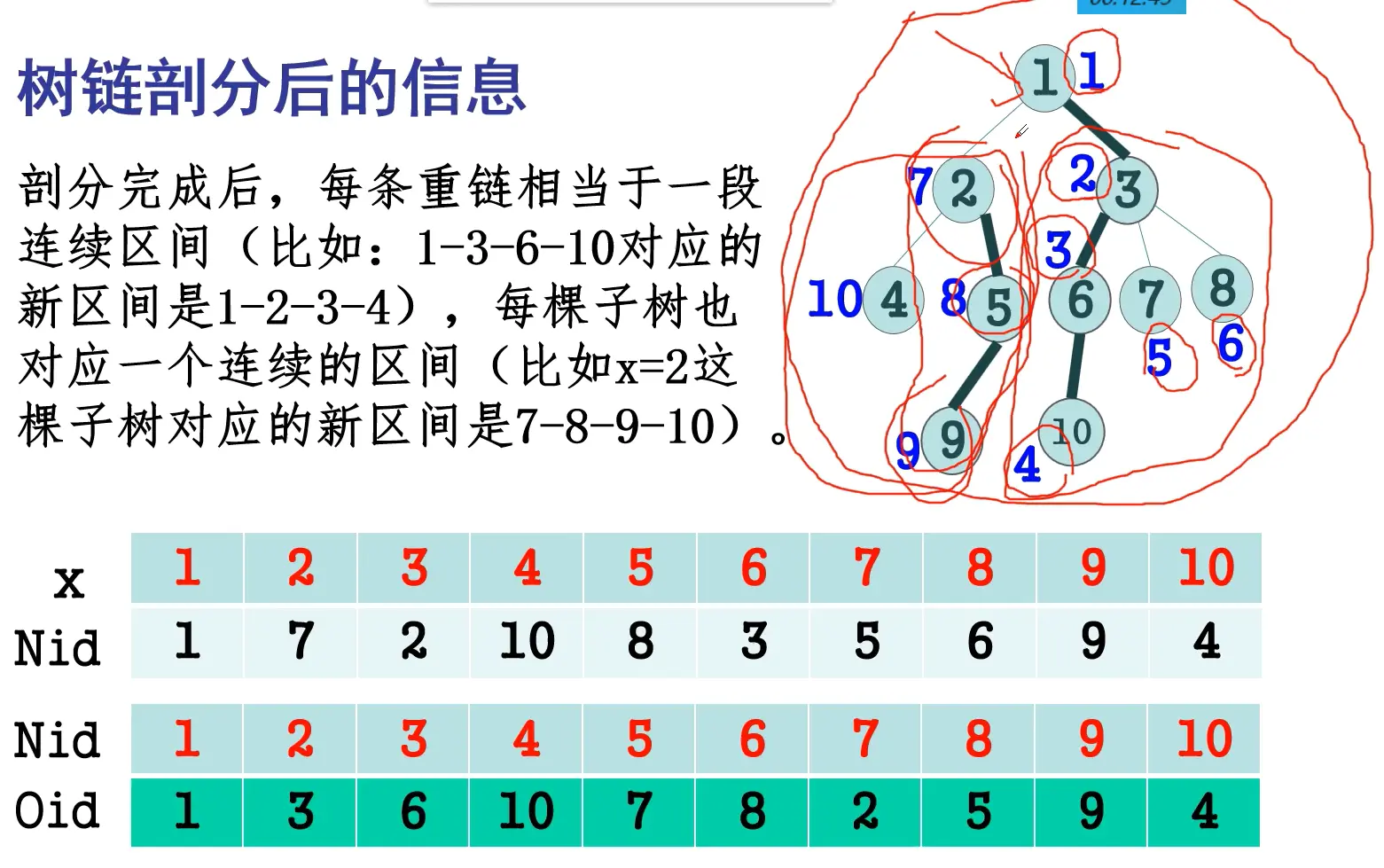
参考代码3(增加新编号的第二次DFS)

int head[N],tot,f[N],d[N],son[N],size[N],top[N],n,m;
int dfn, Nid[N], Oid[N];
struct edge{ int to, nex; } e[N<<1];
void dfs2(int x,int topx){
    top[x]=topx;
    Nid[x] = ++dfn; // 原始元素x对应的DFS序新编号是Nid[x]
    Oid[dfn]=x; // 新编号Nid[x]对应的老编号是x，即Oid[Nid[x]]=x;
    if(son[x]!=0) dfs2(son[x],topx);//先处理重边，确保重链区间连续
    for(int i=head[x]; i; i=e[i].nex){
        if(e[i].to !=f[x] && e[i].to !=son[x])
            dfs2(e[i].to, e[i].to);
    }
} //如果对x为根的整个子树操作，对应区间[Nid[x],Nid[x]+size[x]-1]

//具体操作可以是各种修改，也可以是各种查询
//具体代码要根据实际情况，分别写成不同的函数，但基本套路类似

void chain(int x, int y) {
    while (top[x] != top[y]) {  //不位于同一条重链
        if (d[top[x]] < d[top[y]]) swap(x, y);
        具体处理top[x]到x这一段,比如修改这一段节点的值
        x = f[top[x]];          //将 x 往上跳过一条轻边
    }
    if (d[x] > d[y]) swap(x, y);
    具体处理 x 到 y 这一段,比如修改这一段节点的值
}

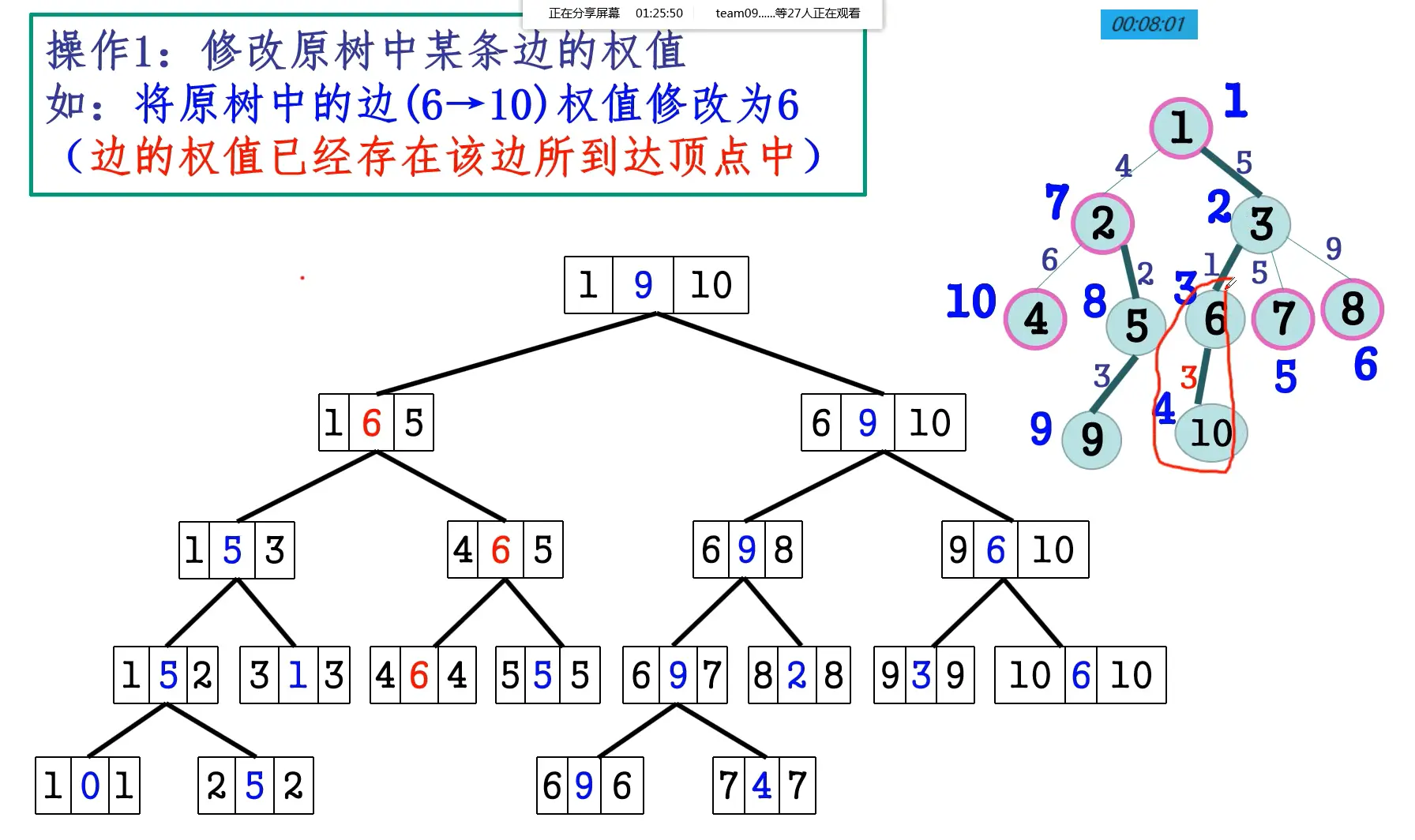
解释：

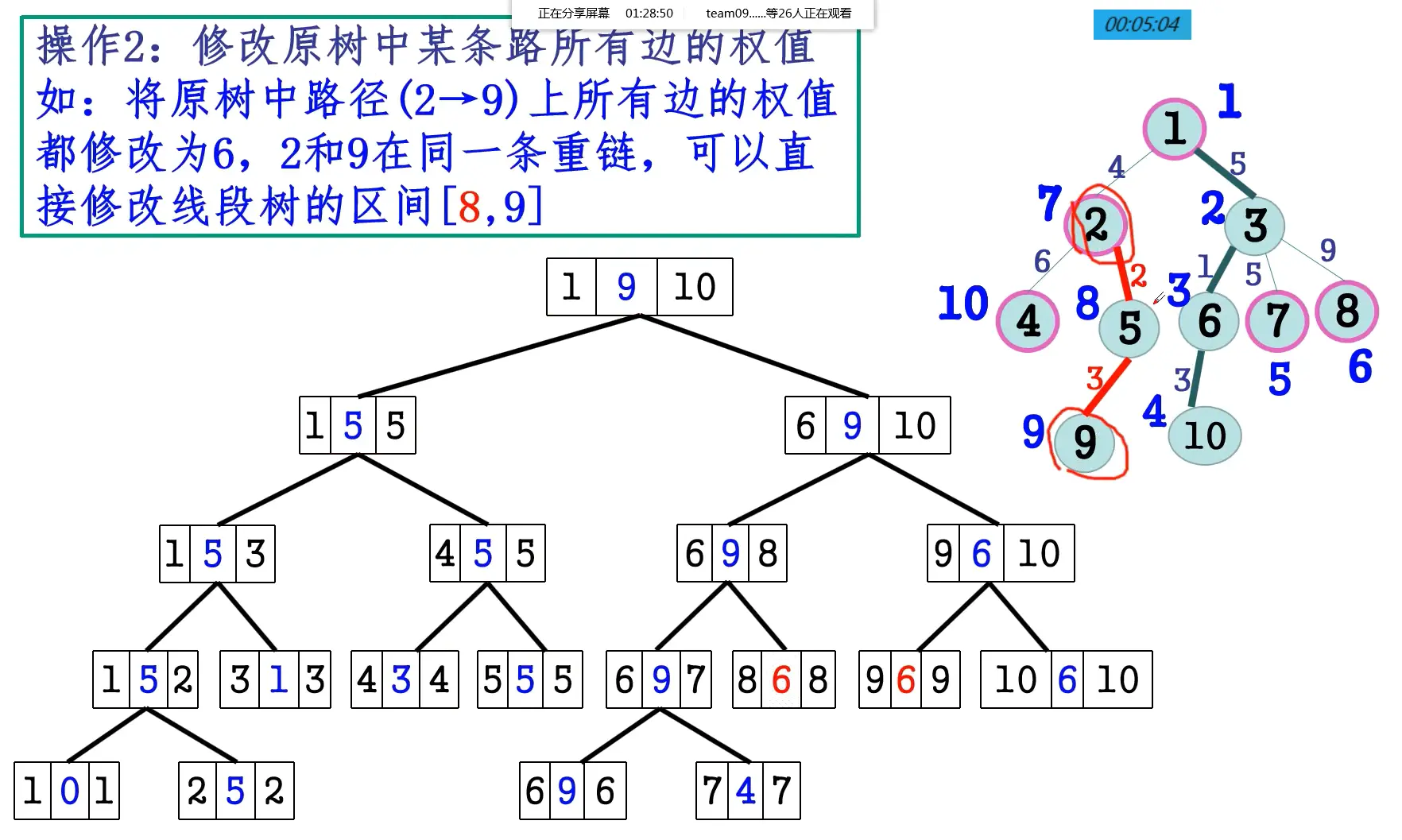
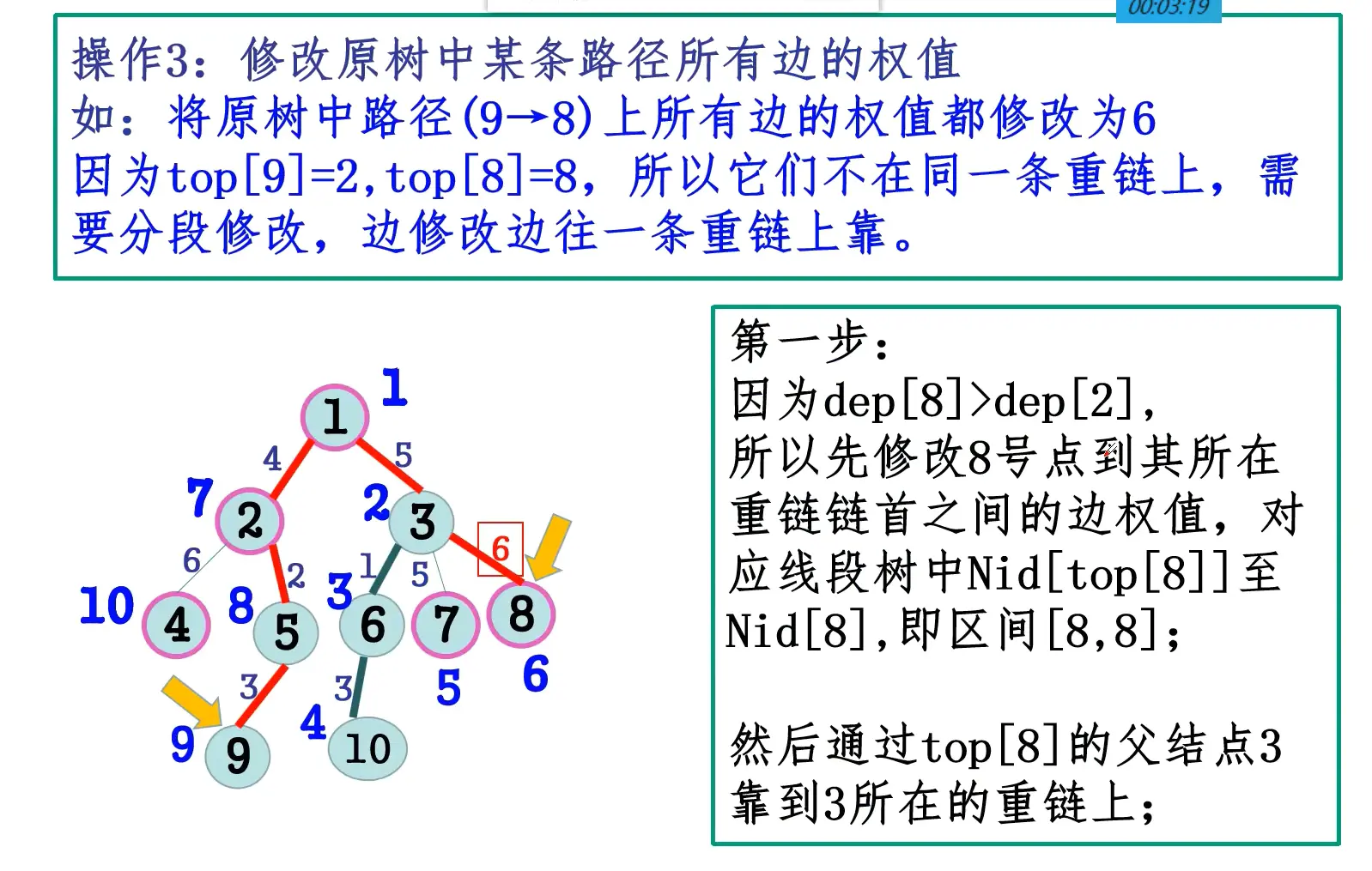
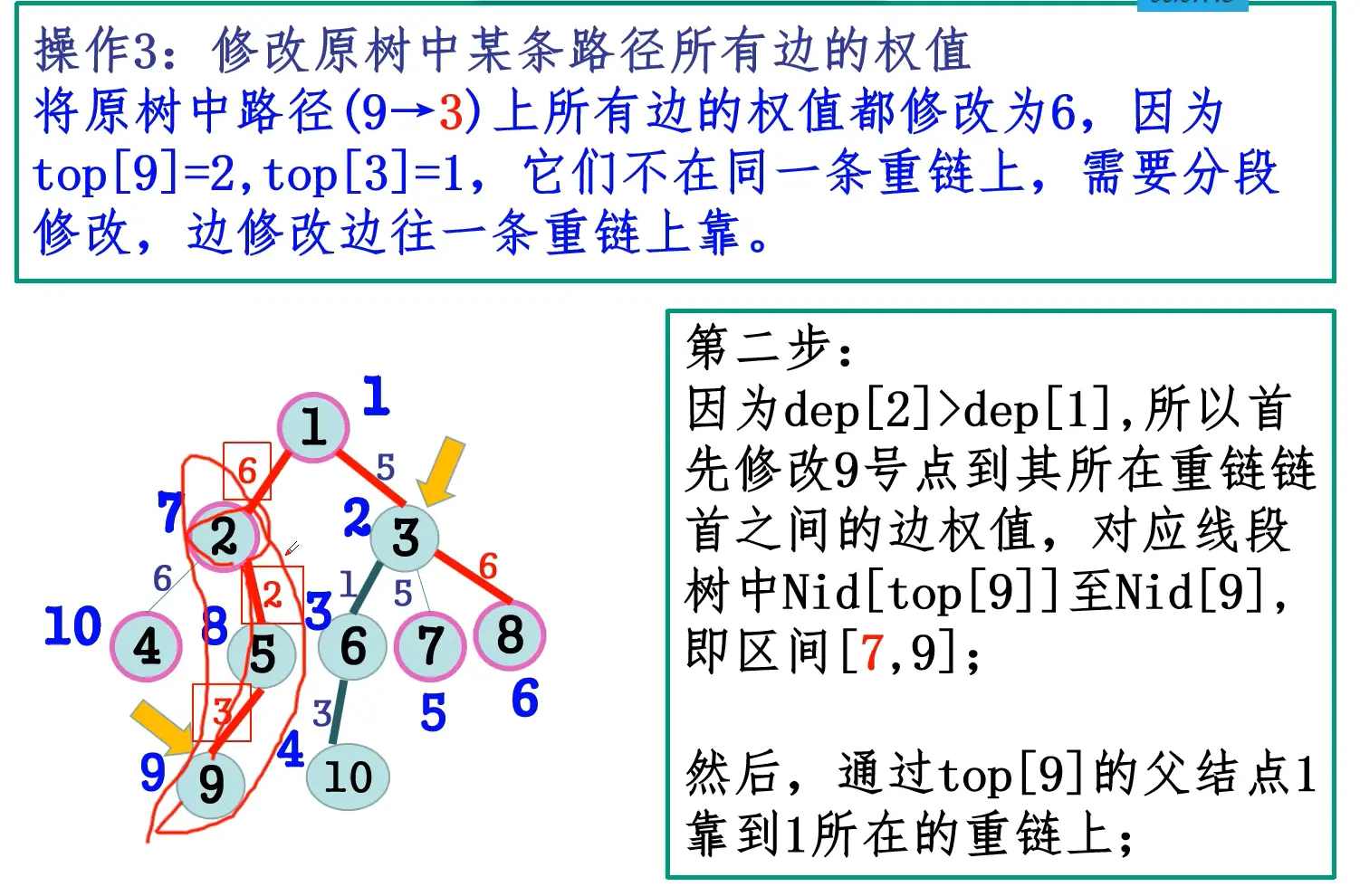
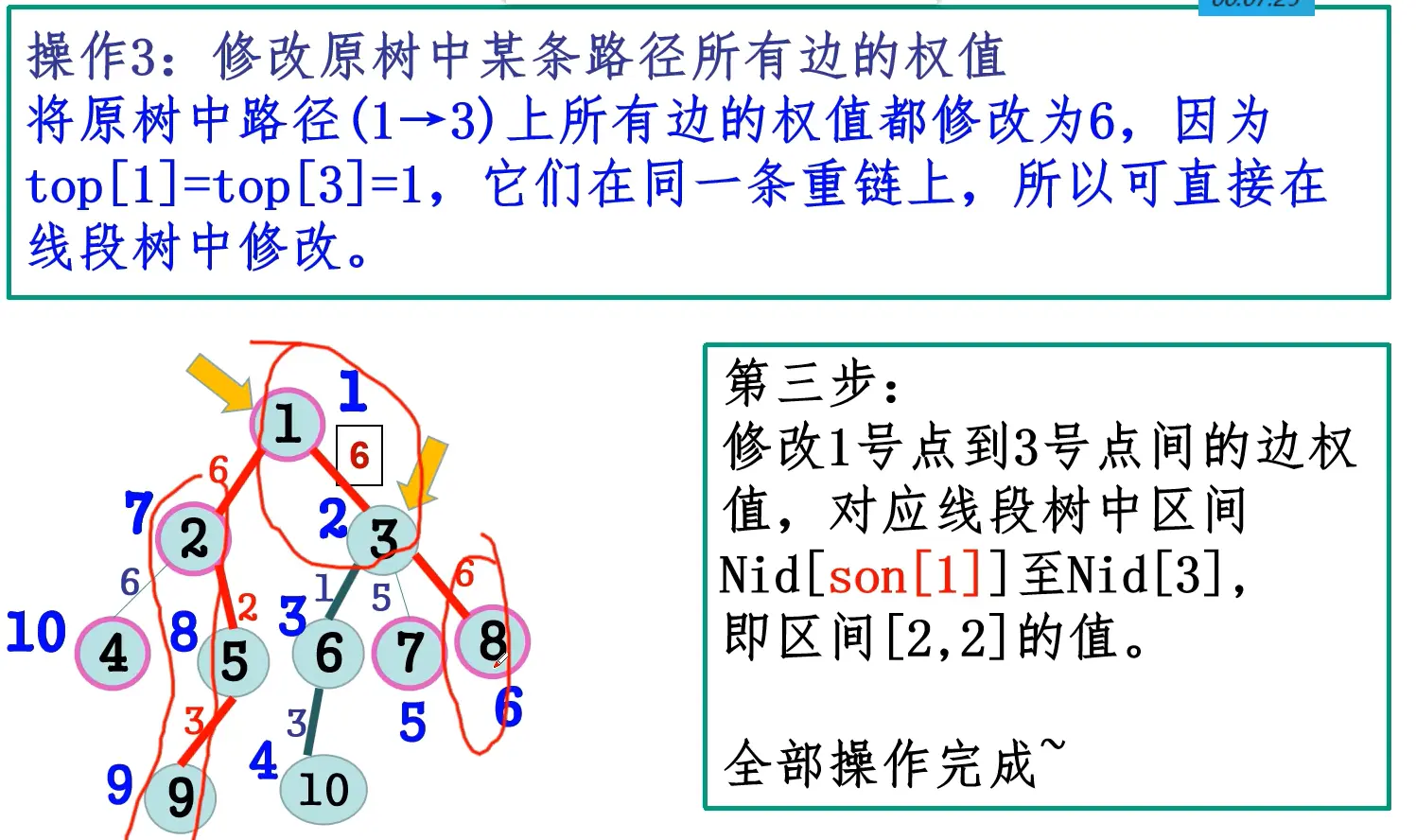
总结

树链剖分-总结

  • 树链剖分的应用场景？ ——LCA，以及各种关于树上路径的操作（更新、查找）

  • 树链剖分的核心操作？
    ——size[x]、d[x]、f[x]、son[x]、top[x]的定义，
    ——两次DFS，以及具体问题的树链操作（更新、查找）

  • 树链剖分的常见搭档？ ——树的子树或路径操作，常转化为线段树的区间操作