倍增算法

发表于 2023-02-11 更新于 2025-07-29 分类于程序设计竞赛

倍增算法

关联复习-树链剖分

树链剖分的应用场景？（树的路径操作、子树的操作）

LCA（Least Common Ancestors），即最近公共祖先。是指这样一个问题：在有根树中，找出某两个结点u和v最近的公共祖先（另一种说法，离树根最远的公共祖先）。

RMQ

关于RMQ问题

RMQ（Range Minimum/Maximum Query），即区间最值查询。是指这样一个问题：对于长度为n的数列A，回答若干询问RMQ（A,i,j）(i,j<=n)，返回数列A中指定区间[i，j]中的最大/小值。

LCA问题和RMQ问题的关系？

LCA《-》RMQ可以互相转换

符号约定

假设一个算法预处理时间为 \(f(n)\)，查询时间为\(g(n)\)。这个算法复杂度的标记为\(\langle f(n), g(n) \rangle\)。

\(\text{RMQ}_A(i, j)\) 来表示数组\(A\)中索引\(i\)和\(j\)之间最小值的位置。

\(\text{LCA}_T(u, v)\) 表示\(u\)和\(v\)的离树\(T\)根结点最远的公共祖先。

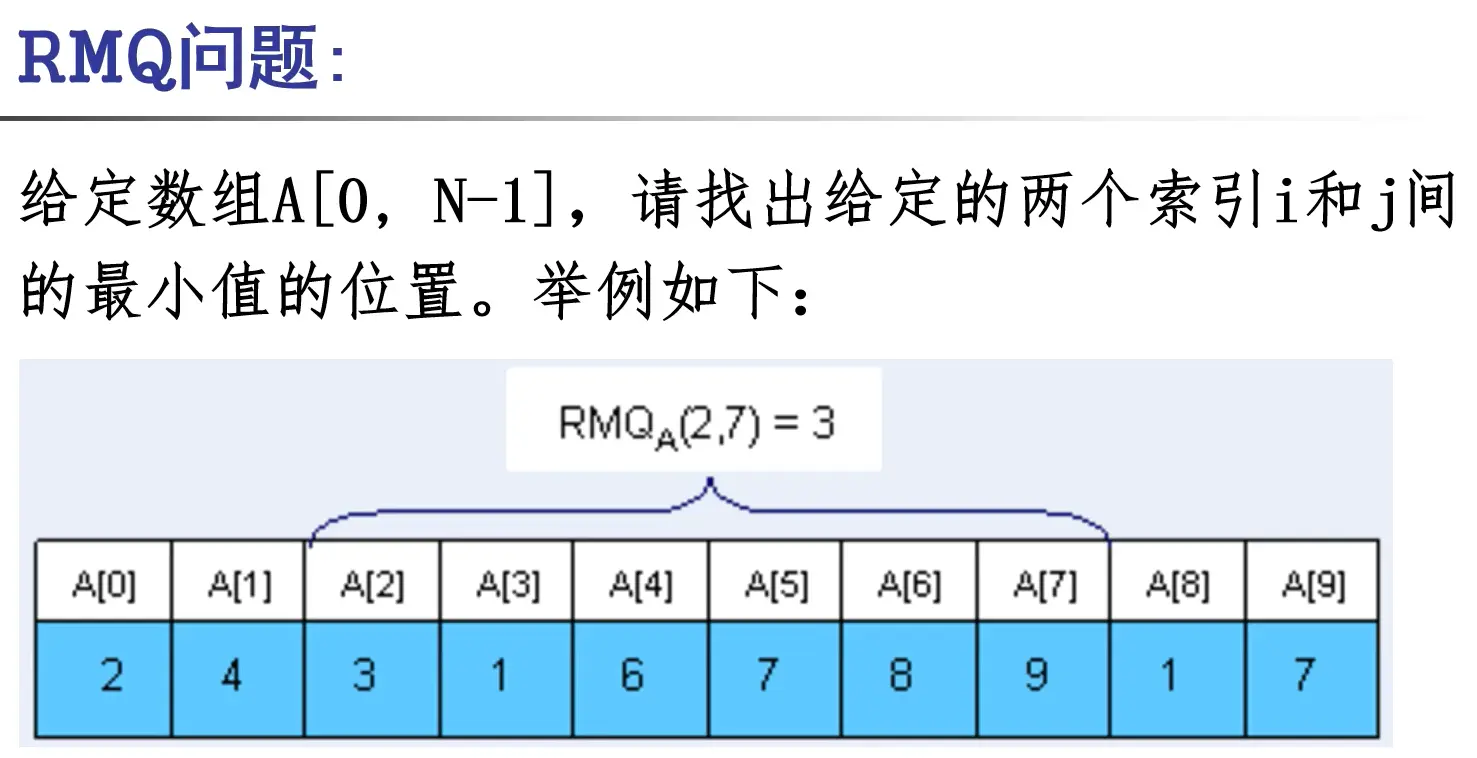
分析：RMQ相关算法

在线暴力遍历算法：

假设数据的规模：N，查询数Q

单次查询时间复杂度：\(O(\mathrm{N})\)

总的时间复杂度：\(O(\mathrm{N*Q})\)

缺点：当查询量特别大的时候（比如，Q>N）？

预处理 + 直接查询：

预处理：枚举所有区间\([i,j]\)，然后每个区间遍历查找复杂度：\(\langle O(N^3),\ O(1) \rangle\)

预处理的DP优化？（请思考并回答）复杂度：\(\langle O(N^2),\ O(1) \rangle\)，而且空间复杂度也是\(O(N^2)\)

优缺点：查询效率高，预处理效率太低

线段树

还想到什么算法？

刚刚学过的线段树！

复杂度？ \(\langle O(n), O(\log n) \rangle\)

分块

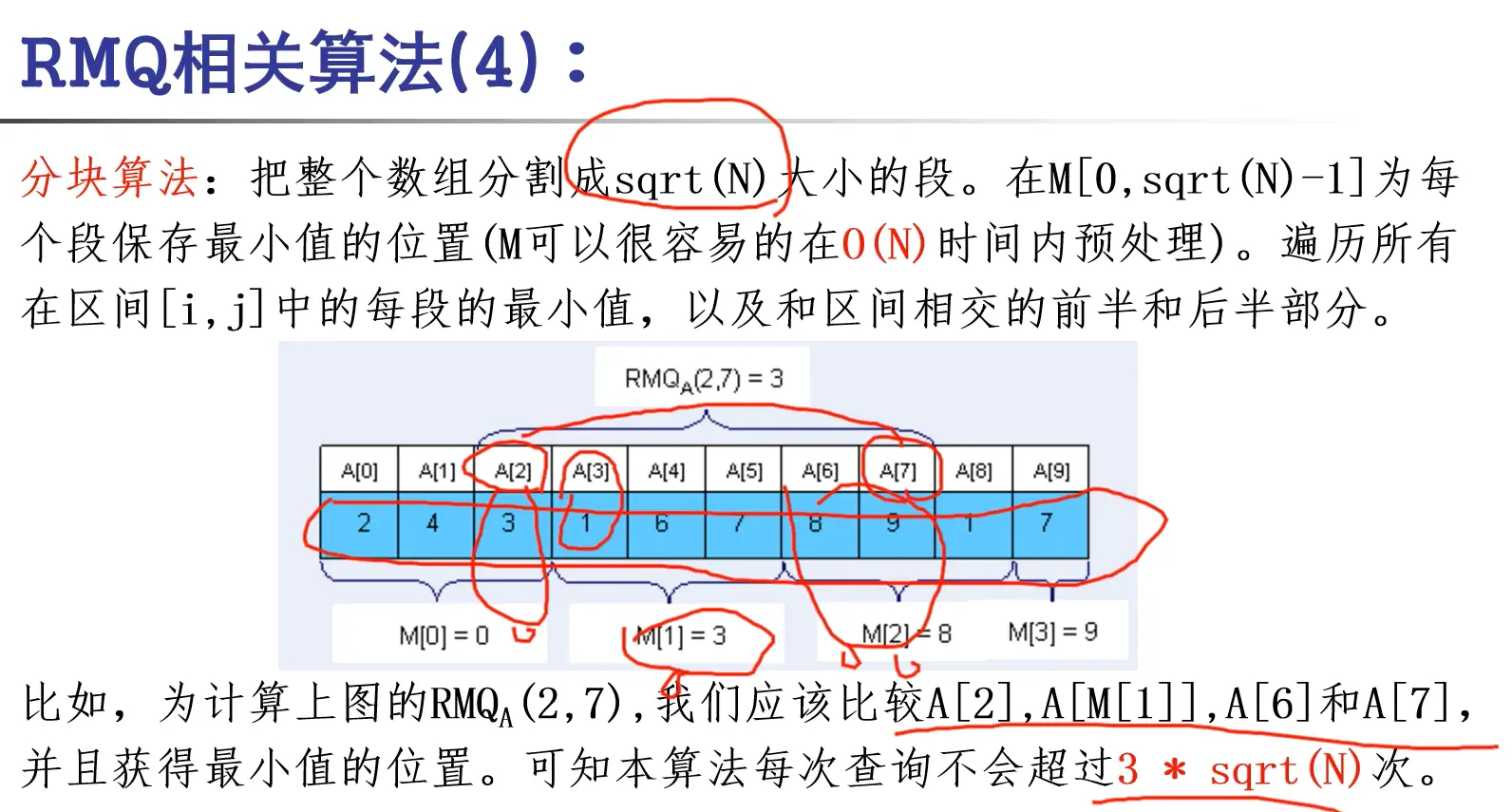
ST表

ST表意为分散表

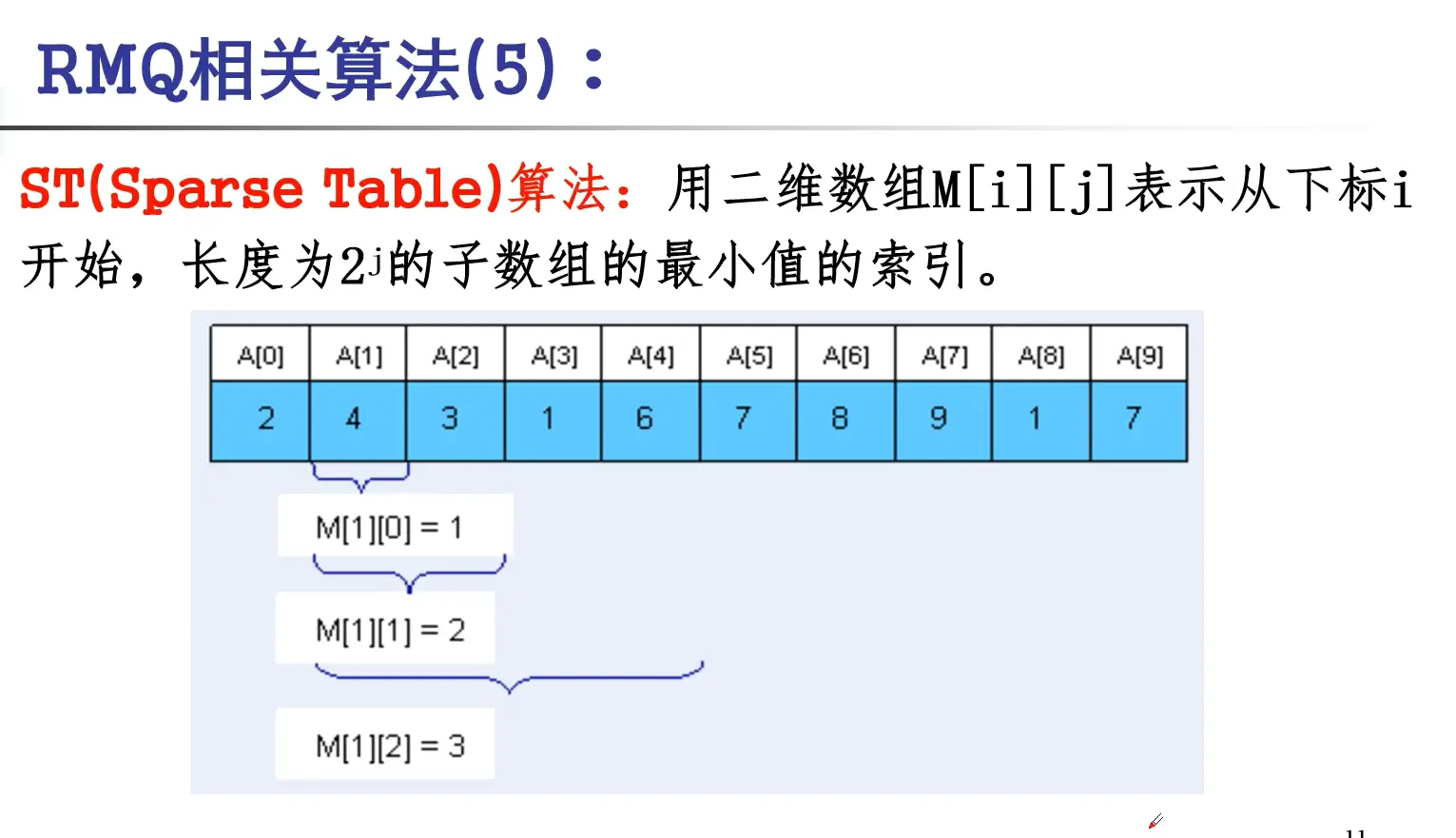
ST算法的DP预处理：

把M[i][j]对应的区间平均分成两段（M[i][j]对应的区间长度一定为偶数），从i到\(i+2^{j-1}-1\)为前一段，\(i+2^{j-1}\)到\(i+2^j-1\)为后一段（长度都为\(2^{j-1}\)），则M[i][j]就是这两段的最小值中的最小值对应的索引。

可得DP状态转移方程：

\[ M[i][j] = M[i][j-1] \quad \text{if}(a[M[i][j-1]] < a[M[i+2^{j-1}][j-1]]) \]

\[ M[i][j] = M[i+2^{j-1}][j-1] \quad \text{else} \]

其中，初始化：\(M[i][0] = i\)

DP递推得到ST表M

ST算法的查询实现：

预处理\(M[i][j]\)完成以后，如何进行\(\text{RMQ}_A(i,j)\)查询？

查询实现：选择两个能够完全覆盖区间\([i..j]\)的块，并且找到它们之间的最小值。设\(k = \lfloor \log_2(j-i+1) \rfloor\)，则得：

\(\text{RMQ}_A(i,j)=M[i][k],\quad \text{if}(a[M[i][k]]<a[M[j-2^k+1][k]])\)

\(\text{RMQ}_A(i,j)=M[j-2^k+1][k],\quad \text{else}\)

\(M[i][k]\)——从查询区间起始点\(i\)开始，向后长度为\(2^k\)的一段

\(M[j-2^k+1][k]\)——从查询区间尾\(j\)开始，向前长度为\(2^k\)的一段

算法复杂度：\(\langle O(N\log N),\ O(1) \rangle\)

k是最长可行区间

倍增求LCA

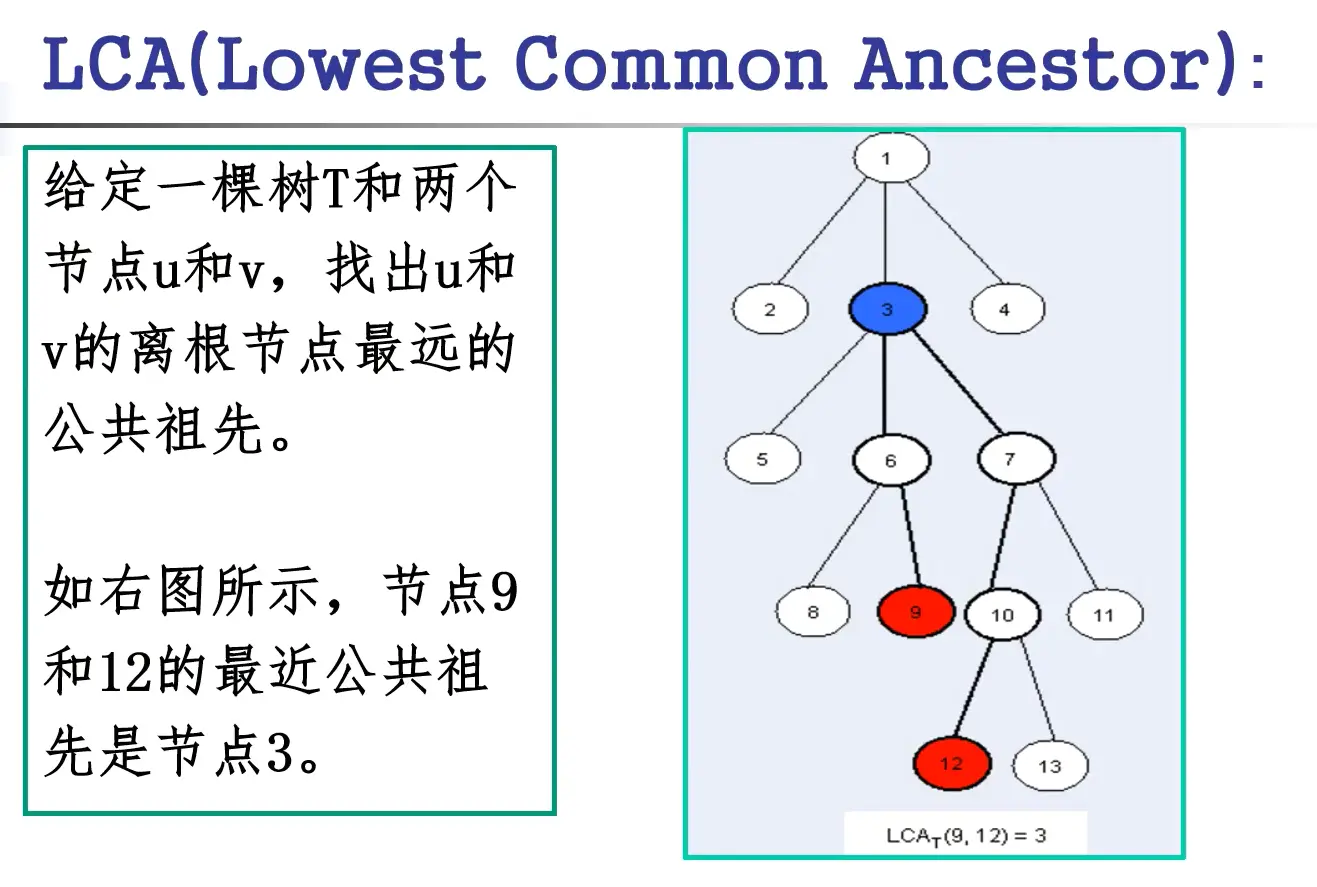
LCA 相关算法分析：

暴力算法1：

分别从节点u和v回溯到T的根节点，获取u和v到根节点的路径P1，P2，其中P1和P2可以看成两条单链表。然后依次判断P1中的每个节点是否在P2中出现，第一个出现在P2中的节点即为第一个相交节点，即\(\text{LCA}_T(\text{u},\text{v})\)。

时间复杂度：\(O(\text{N}^2)\) 为什么？

暴力算法2：

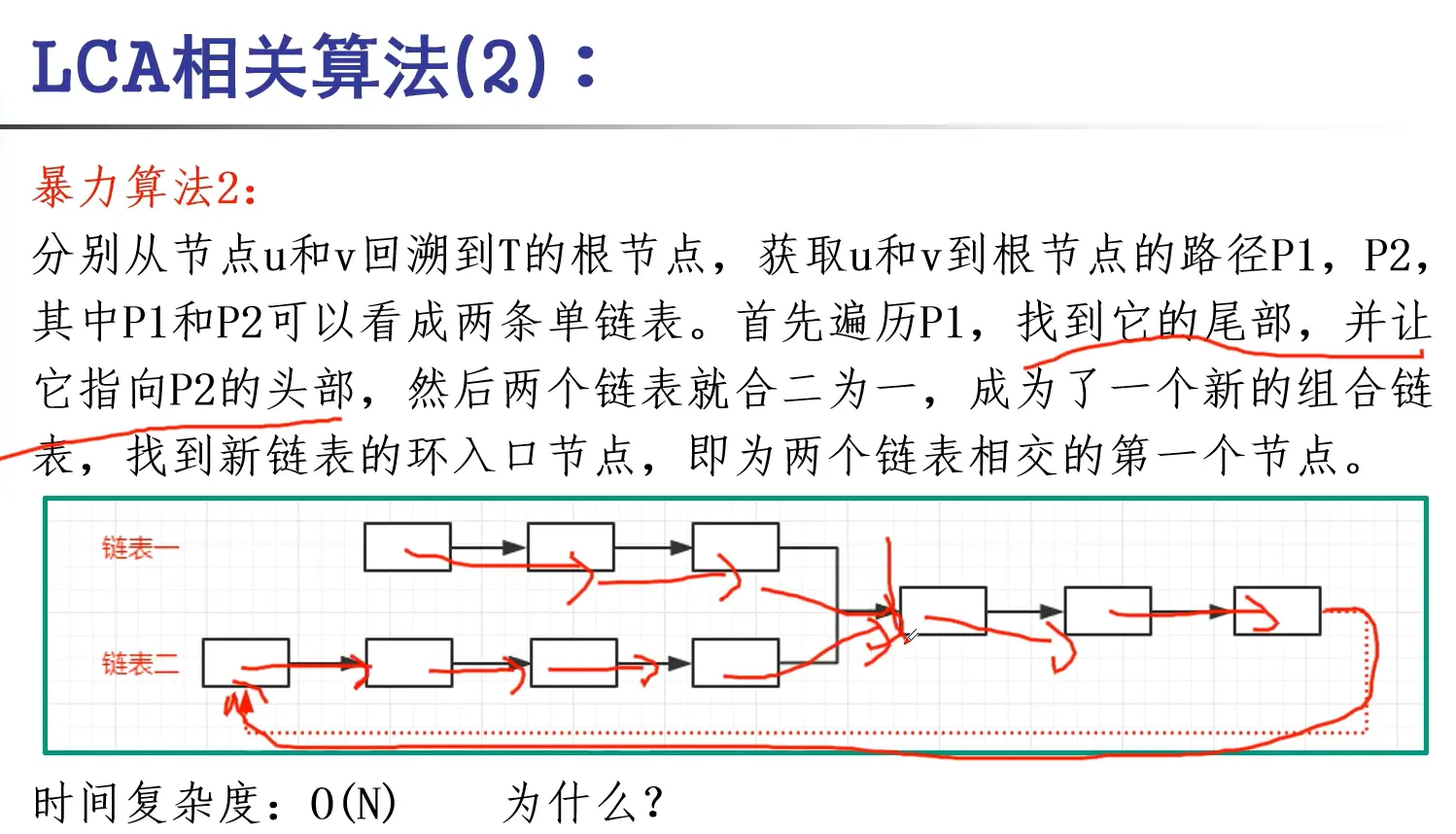
访问过做标记，走到做过标记的点就是公共祖先

倍增算法

算法思路：
首先，将x和y中深度较大的那个往上跳到和另一个深度相同。
此时，如果x=y，则LCA(x,y)=x，算法结束，否则进入下一步。
然后，同时向上倍增枚举一个2的幂的步长\(2^i\)，若x往上走\(2^i\)步与y往上走\(2^i\)步不为同一个点，则将它们同时往上走\(2^i\)步。
循环类似处理（逐步缩小i）
最后，你会发现，LCA(x,y)=father[x]=father[y]。

时间复杂度：\(\langle O(N\log N), O(\log N) \rangle\)

算法实现：

预处理P[i][j]（表示结点i的第\(2^j\)个祖先）

P[i][j]的DP状态转移方程为：
P[i][0]=father[i]
P[i][j]=P[P[i][j-1]][j-1]

预处理时间复杂度：\(O(n\log n)\)

代码：

int father[MAXN], P[MAXN][LOGMAXN],int L[MAXN];
void PreProcess(int N)
{ for (int i = 0; i < N; i++)
      for (int j = 0; 1 << j < N; j++)
          P[i][j] = -1;
  for (int i = 0; i < N; i++)
      P[i][0] = father[i];
  for (int j = 1; 1 << j < N; j++)
      for (int i = 0; i < N; i++)
          if (P[i][j - 1] != -1)
              P[i][j] = P[P[i][j-1]][j-1];
}

最后三行可以改写

int LCA(int u, int v)
{
    int tmp, log, i;
    if (L[u] < L[v]) swap(u, v);         // 让u是距离根更远的那个
    for (log = 1; 1 << log <= L[u]; log++); // 注意最后的分号
    log--;                               // log保存的值是？
    //下面的for循环结束后，u和v位于同一层次
    for (i = log; i >= 0; i--)
        if (L[u] - (1 << i) >= L[v])    u = P[u][i];
    if (u == v)     return u;   //特殊情况v就是u的祖先，移到同层即搞定
    for (i = log; i >= 0; i--) //该循环处理一般情况，结束后u和v位置是？
        if (P[u][i] != -1 && P[u][i] != P[v][i])
            u = P[u][i], v = P[v][i];
    return father[u];
}

log 是最大的上升 \(2^{log}\) 层数可依据小样例来尝试一下

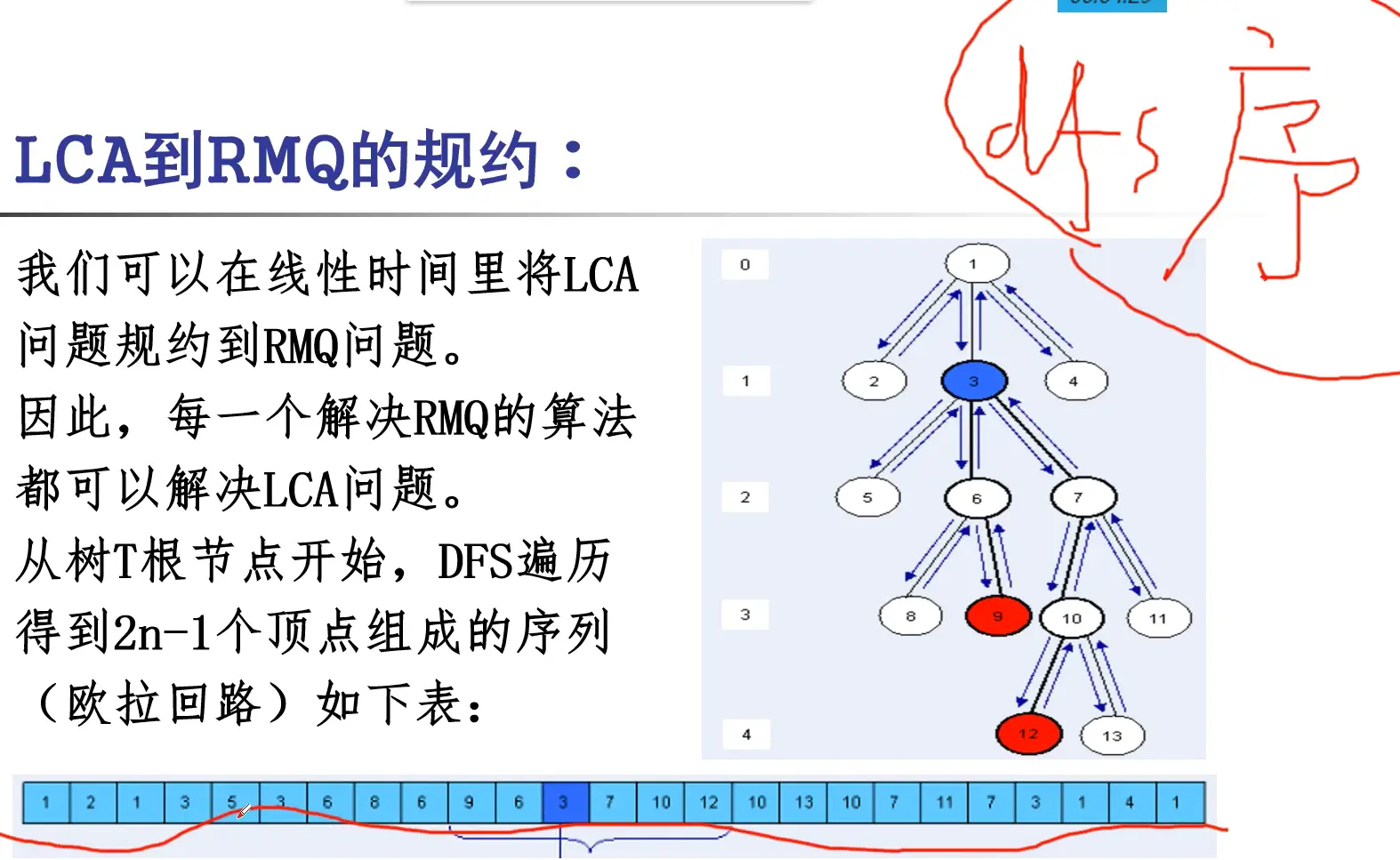
RMQ(DFS+ST)

DFS+ST算法（基本思想：\(\text{LCA}_T(\text{u},\text{v})\) 是在对T进行dfs过程当中u和v之间离根结点最近的点）考虑树的欧拉环游过程中u和v之间所有的结点，并找到它们之间处于最低层的结点。为此，我们建立三个数组：

\(\text{E}[1, 2*\text{N}-1]\) －对T进行欧拉环游过程中所有访问到的结点； \(\quad\quad\quad\quad\quad\quad\quad\ \text{E}[i]\) 是在环游过程中第i个访问的结点

\(\text{L}[1, 2*\text{N}-1]\) －欧拉环游中访问到的结点所处的层数； \(\quad\quad\quad\quad\quad\quad\quad\ \text{L}[i]\) 是\(\text{E}[i]\)所对应的层数（思考：如何计算\(\text{L}[i]\)？）

\(\text{H}[1, \text{N}]\) － \(\text{H}[i]\)是\(\text{E}\)中结点i第一次出现的下标；（任何出现i的地方都行，当然选第一个最方便）

dfs序列中使用st表找到深度最浅的点，这里就是是LCA点

小结：

Q询问次数20万以上最好用O（1）

致谢

本讲部分内容参考了以下资料：

http://dongxicheng.org/structure/lca-rmq/

https://www.cnblogs.com/drizzlecrj/archive/2007/10/23/933472.html

（注意：资料为翻译文章，但是部分细节有笔误）

https://blog.csdn.net/m0_37809890/article/details/82856158

eg1-cd指令

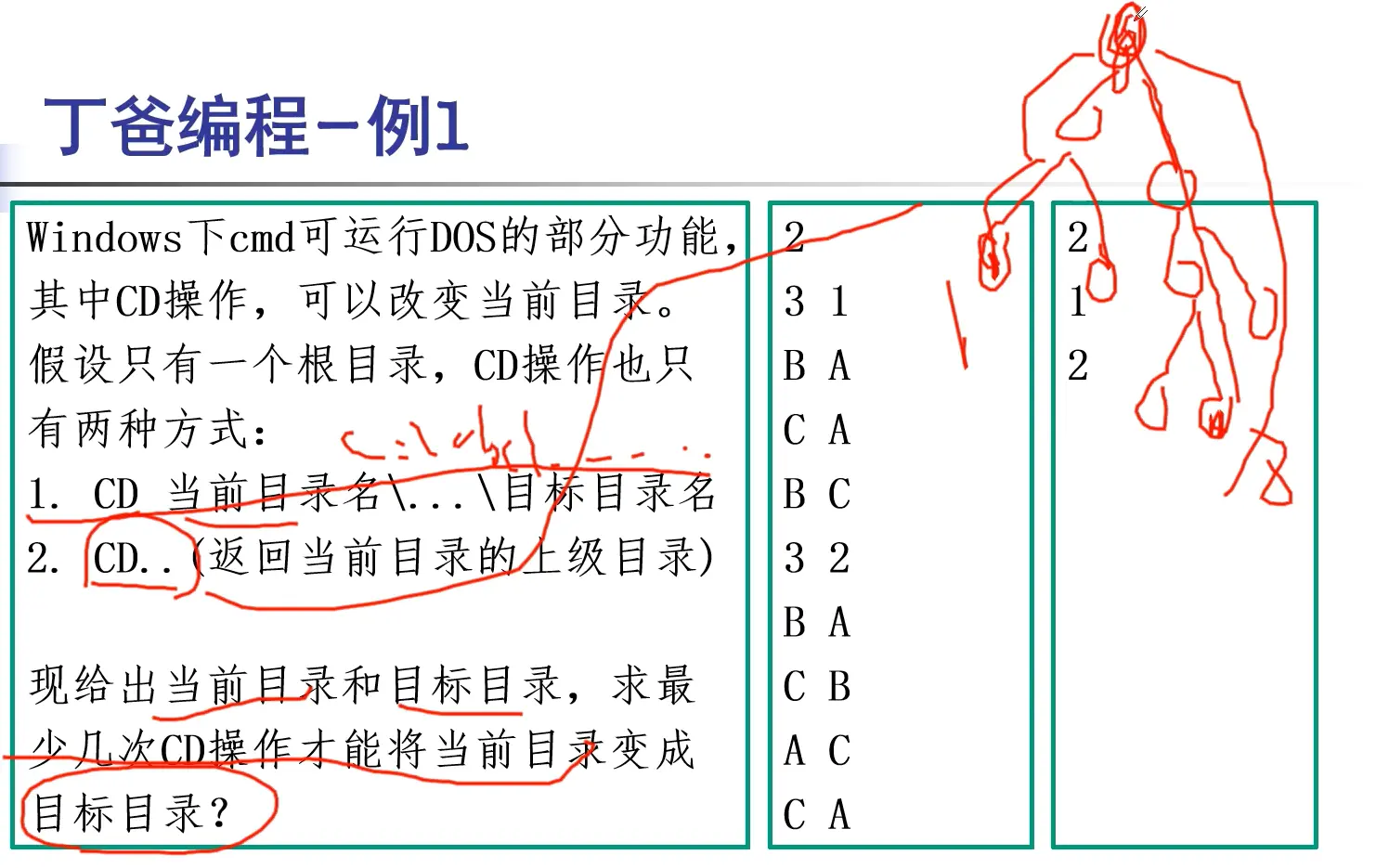
解法：

问题本质：求出目录A到B所需要的CD操作次数

细节提醒：这里的A B为字符串，可考虑用map映射

然后，直接求LCA，分情况讨论即可：
1、A=B，需要的CD操作数是0；
2、A是B的祖先节点，则A–>B的CD操作数是1；
3、B是A的祖先节点，则A–>B的CD操作数是 \(\text{deep}[A] - \text{deep}[B]\)；
4、若互相不是对方祖先，则CD操作数是 \(\text{deep}[A] - \text{deep}[\text{lca}(A,B)] + 1\)；

需要Map映射

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <map>
using namespace std;
#define ll long long

int t,n,m;
string a,b;
map<string,int> mp; 
struct node {
    int to;
    int next;
};
node edge[100010];
int head[100010];
int cnt=0;
int g[100010];
int d[100010];
int sizes[100010];
int son[100010];
int f[100010];
int top[100010];

void addedge(int from,int to){
    edge[++cnt].to=to;
    edge[cnt].next=head[from];
    head[from]=cnt;
    return ;
}

void dfs1(int x,int fa){
    sizes[x]=1;
    f[x]=fa;
    son[x]=0;
    d[x]=d[fa]+1;
    for(int k=head[x];k!=0;k=edge[k].next){
        int to=edge[k].to;
        // if(to==fa){
        //  continue;
        // }
        dfs1(to,x);
        sizes[x]+=sizes[to];
        if(sizes[son[x]]<sizes[to]){
            son[x]=to;
        }
    }
    return ;
}

void dfs2(int x,int topx){
    top[x]=topx;
    if(son[x]!=0){
        dfs2(son[x],topx);
        // return ;
    }
    for(int k=head[x];k!=0;k=edge[k].next){
        if(edge[k].to!=son[x] && edge[k].to!=f[x]){
            dfs2(edge[k].to,edge[k].to);
        }
    }
    return ;
}

int lca(int x,int y){
    // cout<<x<<" "<<y<<"ORI"<<endl;
    // cout<<"TOP:::"<<top[x]<<" "<<top[y]<<endl;
    while(top[x]!=top[y]){
        if(d[top[x]]<d[top[y]]){
            int temp=x;
            x=y;
            y=temp;
        }
        x=f[top[x]];
    }
    // cout<<x<<" "<<y<<endl;
    return d[x]>d[y]?y:x;
}

int main(){
    cin>>t;
    while(t--){
        //clear
        int num=0;
        mp.clear();
        cnt=0;
        memset(head,0,sizeof(head));

        cin>>n>>m;
        for(int i=1;i<n;i++){
            cin>>a>>b;
            if(mp[a]==0){
                mp[a]=++num;
            }
            if(mp[b]==0){
                mp[b]=++num;
            }
            // cout<<a<<" "<<mp[a]<<endl;
            // cout<<b<<" "<<mp[b]<<endl;
            addedge(mp[b],mp[a]);
            g[mp[a]]++;
        }

        int root=0;
        for(int i=1;i<=n;i++){
            if(!g[i]){
                root=i;
                break;
            }
        }
        dfs1(root,0);
        //test:
        // for(int i=1;i<=n;i++){
        //  printf("%d %d %d %d\n",f[i],son[i],sizes[i],d[i]);
        // }
        // cout<<root<<endl;
        // cout<<endl;

        dfs2(root,root);

        for(int i=1;i<=m;i++){
            cin>>a>>b;
            int start=mp[a];
            int to =mp[b];
            int anc=lca(start,to);
            int ans=0;
            if(start!=anc){
                ans+=d[start]-d[anc];
            }
            if(to!=anc){
                ans++;
            }
            // cout<<anc<<endl;
            printf("%d\n",ans);
        }

    }
    return 0;
}