强连通分量

例题一

• 给定一个有向图，统计有多少点对u, v(u<v)满足： u可以到达v，且v可以到达u。

• 思考：如何解决？

• 暴力？复杂度不可想象…

强连通分量定义

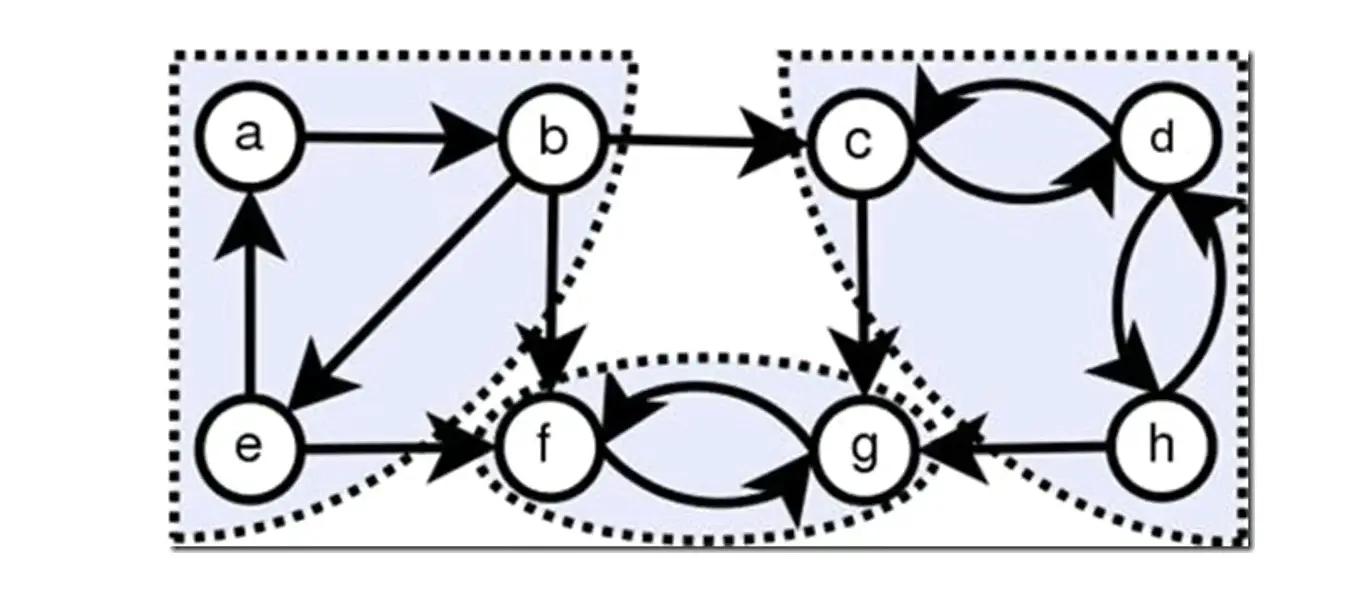
在一个有向图中，选取一个点集S，如果对于S中的任意两点u, v都满足u可以到达v，则称S是强连通的。

如果一个强连通点集S中，不能再加入更多的点使得它仍然强连通，则称S是强连通分量。

## 需要的算法

求强连通分量的算法

1. Tarjan：\(O(n+m)\)，细节较多。

2. Kosaraju：\(O(n+m)\)，细节较少，可以继续优化。

Kosaraju算法

Kosaraju算法求强连通分量

在无向图中，求解连通分量只需要按照1到n的顺序依次考虑每个点。

考虑到i点时，如果i点未被访问过，就说明找到了一个新的连通分量，从i点开始DFS即可找到i所在的连通分量。

所以——无向图的连通分量数等价于对整个图的遍历进行了几次（最外层的）DFS。

无向图DFS即可计算出，还可以并查集计算 在有向图中：

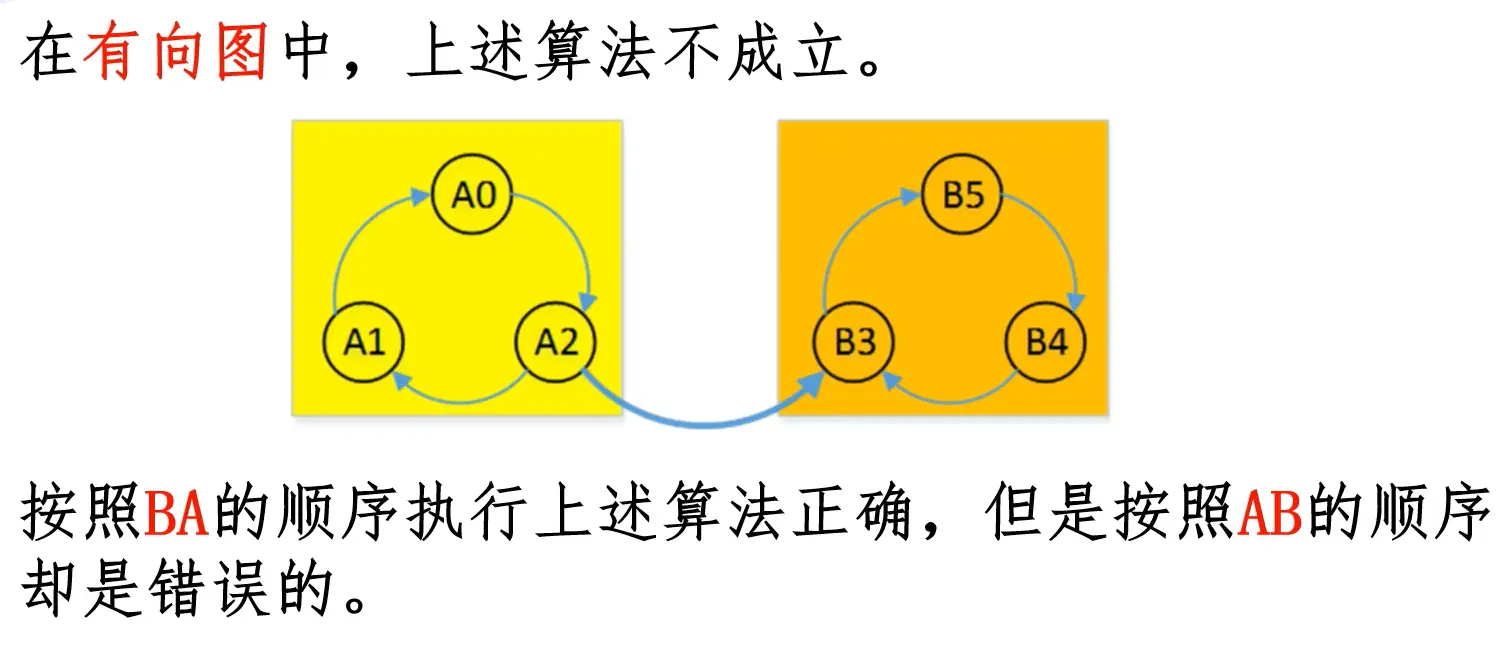
解决方法 转化问题，到DFS

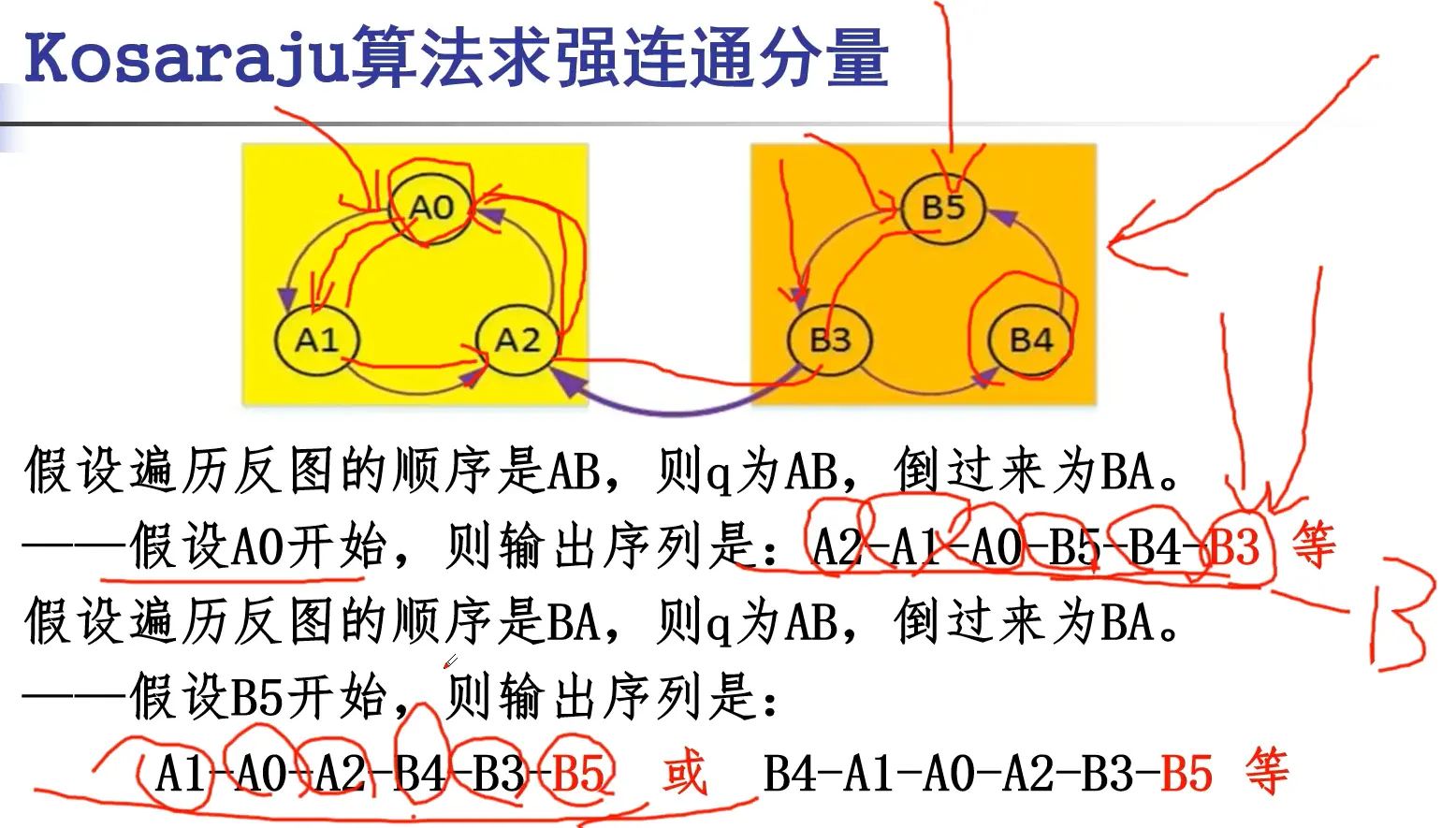
Kosaraju算法的思想：

1. 把图中所有边反向，再按照1到n的顺序去DFS（后续遍历），得到每个点的出栈序列q。

2. 按照q[n]..q[1]的顺序去DFS原图就是一个合法的顺序。

第一遍DFS，产生队列（后序遍历）即结束DFS后输出其值，再回溯 序列p一定可行 生成BA可行

简化处理

Kosaraju算法求强连通分量

因为把边反向与否不改变强连通分量，所以得到一个简化的Kosaraju算法：

1. 按照1到n的顺序去DFS后续遍历原图，得到每个点的出栈序列q。
2. 按照q[n]..q[1]的顺序去DFS反图，依次得到每个强连通分量。

代码

Kosaraju算法求强连通分量

void dfs1(int x){
  vis[x]=1;
  for(int i=G[0][x];i;i=NXT[0][i])if(!vis[V[0][i]])dfs1(V[0][i]);
  q[++t]=x;
}
void dfs2(int x,int y){
  vis[x]=0,f[x]=y;
  for(int i=G[1][x];i;i=NXT[1][i])if(vis[V[1][i]])dfs2(V[1][i],y);
}
int main(){
  for(t=0,i=1;i<=n;i++)if(!vis[i])dfs1(i);
  for(i=n;i;i--)if(vis[q[i]])dfs2(q[i],q[i]);
}

上文使用二维数组，0为正，1为反图，y类似于并查集根，v储存的就是to节点

vector代码

vector<int> edge1[100005], edge2[100005], p;

void dfs1(int root)
{
    vis[root] = 1;
    int len = edge1[root].size();
    for(int i = 0; i < len; i++){
        if(!vis[edge1[root][i]]) dfs1(edge1[root][i]);
    }
    p.push_back(root);
}

时间复杂度

Kosaraju算法时间复杂度

一共要对正反图分别进行一轮DFS。

每轮DFS经过\(O(n)\)个点，\(O(m)\)条边。

总时间复杂度\(O(n+m)\)。

例题1解

• 给定一个有向图，统计有多少点对u,v(u<v)满足u可以到达v，且v可以到达u。
• u和v互相可达当且仅当它们属于同一强连通分量。
• 求出强连通分量，假设某个强连通分量有k个点，那么对答案的贡献为\(C(k,2)\)。
• 思考：如何统计强连通分量中元素的个数？
• 时间复杂度\(O(n+m)\)。

统计数量：需要使用y标记时cnt++；

例题二：

• 给定一个有向图，每个点i有点权v[i]，请对于每个点i找到i能到达的点中点权的最大值。
• \(dp[i]=\max(v[i], dp[j])\)，i->j有边。
• 有环怎么办？没法确定DP的顺序。

解决：缩点

• 将强连通分量缩成一个点后的图是个DAG。
• 将每个强连通分量的点权设为内部点权的最大值，然后在DAG上按拓扑序递推或者记忆化搜索即可。
• 时间复杂度\(O(n+m)\)。

f[x]就是一个分量

• 具体怎么实现缩点？
• 设\(f[x]\)表示\(x\)属于哪个强连通分量。
• 对于原图中的边\(x \to y\)，在新图中添加\(f[x] \to f[y]\)的边。
• 注意特判\(f[x] == f[y]\)的情况，需要过滤掉自环。 \(\boldsymbol{DAG}\)

void build3() {  //创建缩点之后的图
  cnt=1; memset(head,0,sizeof(head));
  for(int i=1; i<=m; i++) {
	  if(f[u[i]]!=f[v[i]]) add_edge(f[u[i]],f[v[i]]);
  }
}

生成一个DAG图