KMP 字符串匹配

发表于 更新于 分类于

KMP 字符串匹配

kmp举例

  • 给定字符串A和字符串B，请判断B是否是A的子串（即：A串是否包含B串）
  • 比如，字符串A=“Dingba hen shuai!” 字符串B=“shuai”
  • A串（等待匹配的串），称为主串（母串）
  • B串（用来匹配的串），称为模式串

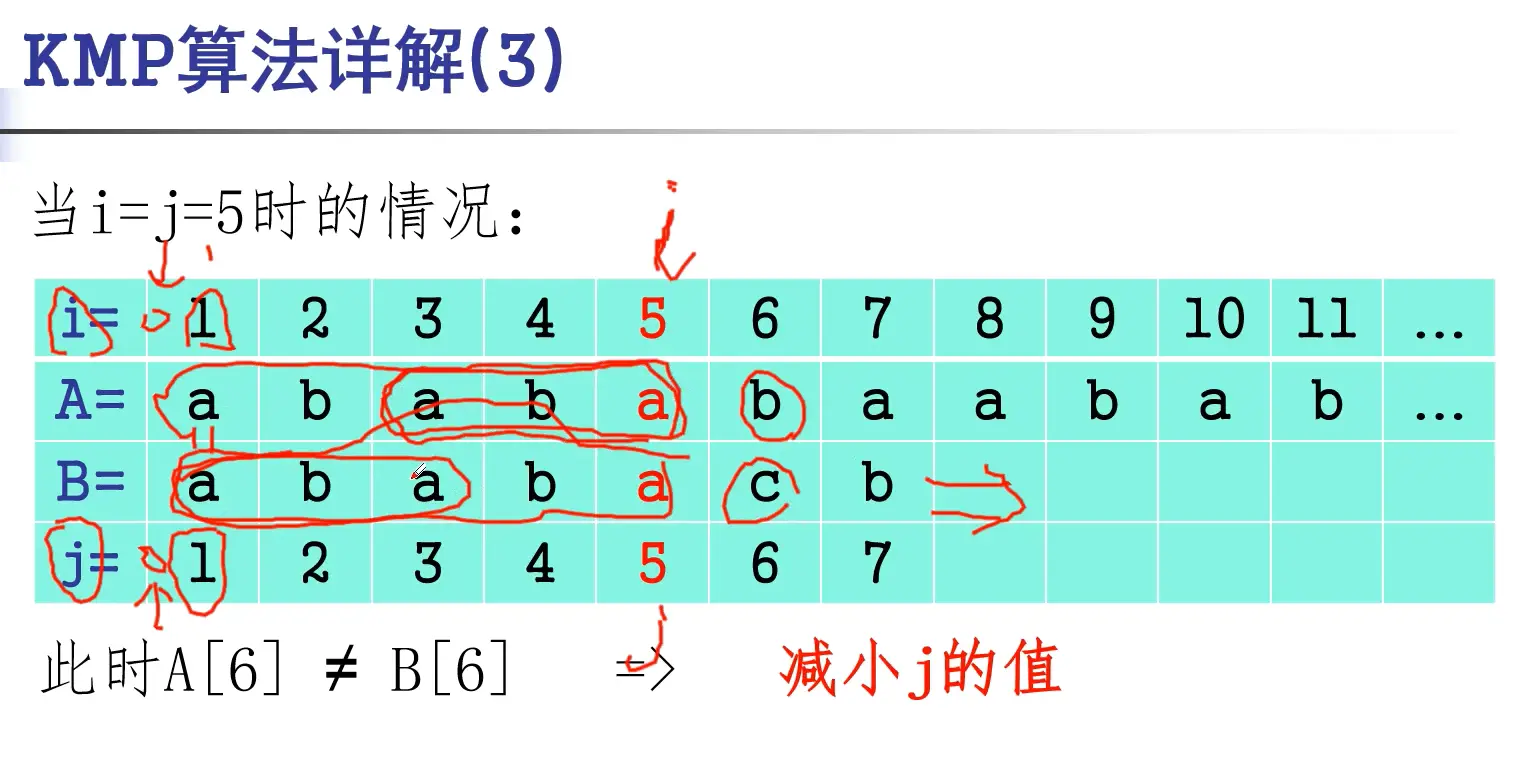
发现 当找到6不匹配时，j减少，相当于向后拉：

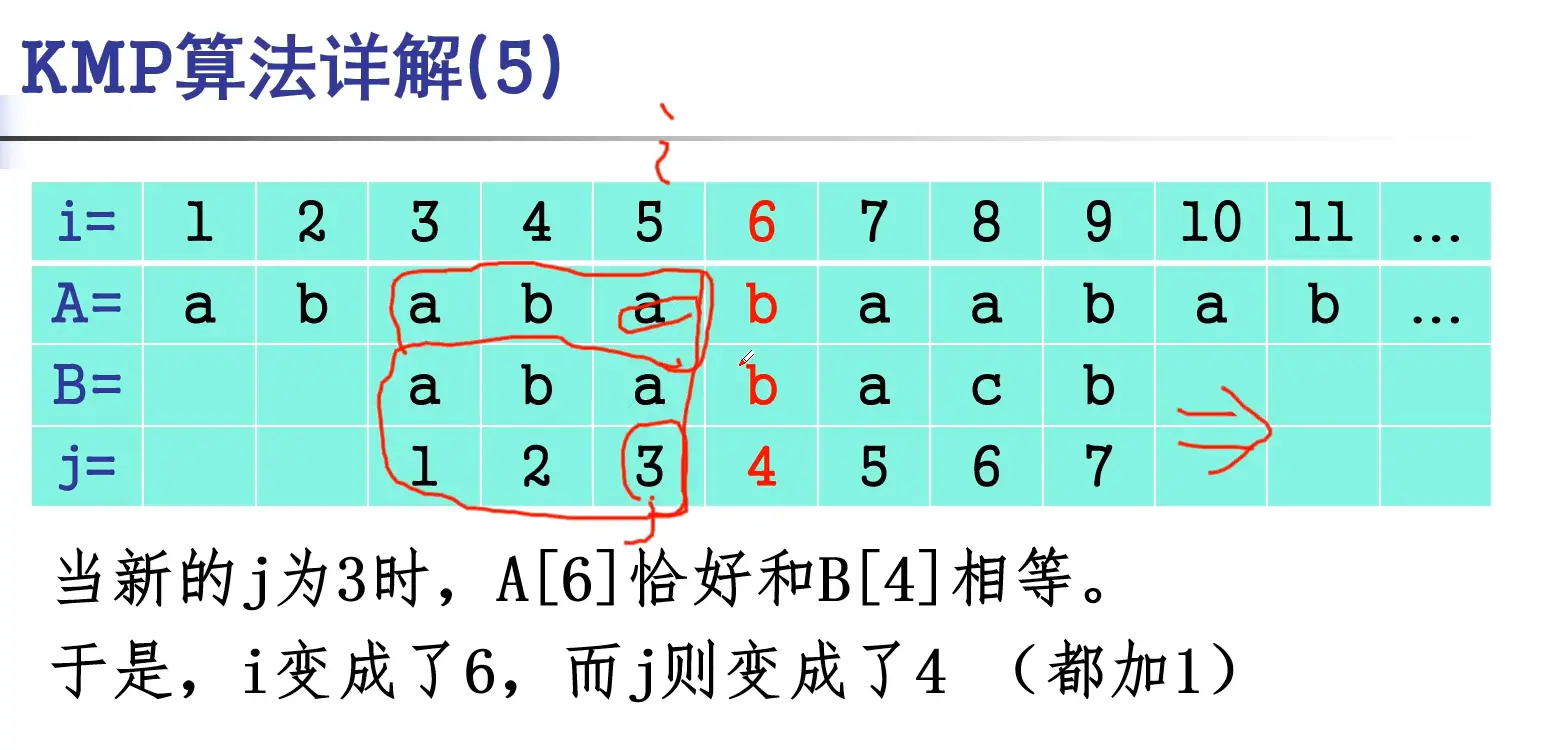
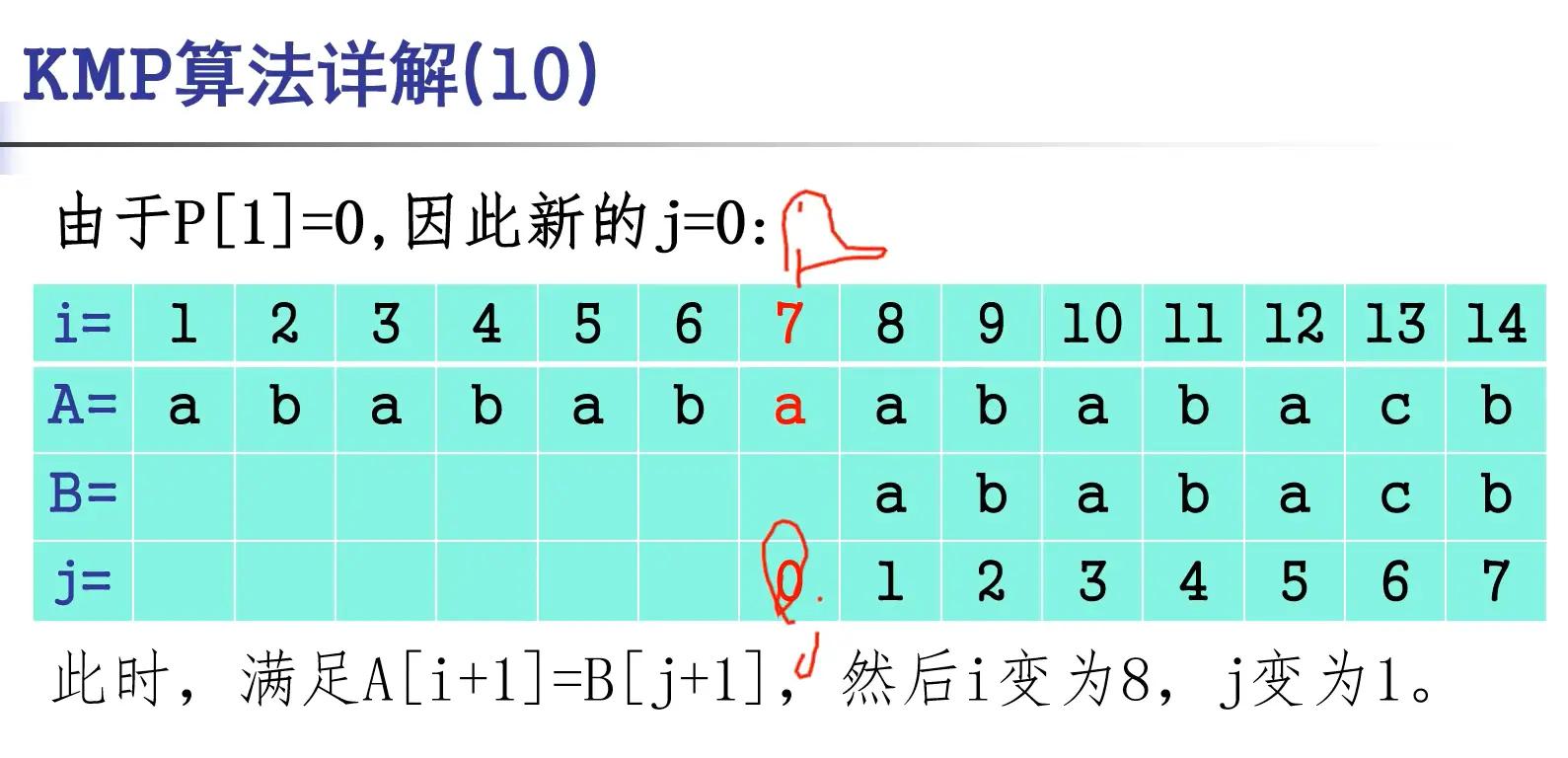
P[]这个数组是当前j位置的前缀和后缀的相同最大长度，便于移动 j

KMP代码

核心

注意：必须使用1开始的下标

//特别提醒：以下算法中的字符串A和B，都是从下标1开始存储
int ans=0, j=0;
for(int i=0; i<n; i++)
{
    while(j>0 && B[j+1]!=A[i+1])
        j=P[j];   //不能继续匹配且j还没减少到0，减少j的值
    if(B[j+1]==A[i+1])  j++;     //能继续匹配，j加1
    if(j==m)                     //找到一处匹配
    {
        printf("%d\n", i-m); //输出子串串首在母串中的位置
        j=P[j];
    }                           //继续寻找匹配（可重叠）
}

上面的代码允许重叠

如果不允许重叠：

j=0即可；

P[]的处理

相当于错位的KMP，对自己做kmp

KMP算法－P数组的预处理

void pre()
{
    P[1]=0;    int j=0;
    for( int i=1; i<m; i++ )
    {
        //不能匹配并且j还没到0，后退一步
        while(j>0 && B[j+1]!=B[i+1]) j=P[j];
        if(B[j+1]==B[i+1])  j++;    //能匹配，j加1
        P[i+1]=j;        //每趟循环求的是i+1位置的值
    }
}//要点：1、B串的自我匹配； 2、计算匹配的长度

小结

一句话理解算法： 扫描字符串A，并更新可以匹配到B的什么位置！

例1-花布条

一块花布条，里面有些图案，另有一块直接可用的小饰条，里面也有一些图案。对于给定的花布条和小饰条，计算一下能从花布条中尽可能剪出几块小饰条来呢？

每组数据占一行，用空格隔开的2个字符串，分别表示花布条和小饰条，'#'结束。

对于每组数据，输出一个整数，表示能从花布条中剪出的最多小饰条的块数。

样例输入
abcde a3
aaaaaa aa
#

样例输出
0
3

解题代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define ll long long

char s1[1010];
char s2[1010];

int p[1010];

void pre(){
    int j=0;
    p[1]=0;
    int m=strlen(s2+1);
    for(int i=1;i<m;i++){
        while(j>0 && s2[i+1]!=s2[j+1]){
            j=p[j];
        }
        if(s2[i+1]==s2[j+1]){
            j++;
        }
        p[i+1]=j;
    }
    return ;
}

int kmp(){
    int ans=0;
    int n=strlen(s1+1);
    int m=strlen(s2+1);
    int j=0;
    for(int i=0;i<=n;i++){
        while(j>0 && s1[i+1]!=s2[j+1]){
            j=p[j];
        }
        if(s1[i+1]==s2[j+1]){
            j++ ;
        }
        if(j==m){
            ans++;
            j=0;
        }
    }
    return ans;
}

int main(){
    while(cin>>(s1+1),s1[1]!='#'){
        cin>>(s2+1); 
        memset(p,0,sizeof(p));
        pre();
        for(int i=0;i<=strlen(s2+1);i++){
            cout<<p[i]<<" ";
        }
        cout<<endl;
        cout<<"ANS::";
        int ans=kmp(); 
        cout<<ans<<endl;
    }
    return 0;
}

例2-pre

  • 题目大意：

给定字符串S1和S2，请查找字符串S1的前缀中同时也是S2的后缀的最大长度是多少。

  • 样例输入：

riemann
marjorie

  • 样例输出：

rie 3

S1+S2求解P值，同时不能超过各个串的长度最小值。 代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
#define ll long long

int p[100010];
string s1;
string s2;
int maxn=0;

void pre(){
    memset(p,-1,sizeof(p));
    int j=-1;
    int n=s1.length();
    for(int i=0;i<n-1;i++){
        while(j>=0 && s1[i+1]!=s1[j+1]){
            j=p[j];
        }
        if(s1[i+1]==s1[j+1]){
            j++;
        }
        p[i+1]=j;
    }
}

int main(){
    while(cin>>s1>>s2){
        maxn=min(s1.length(),s2.length());
        s1+=s2;
        pre();
        int x=min(maxn,p[s1.length()-1]+1);
        for(int i=0;i<x;i++){
            cout<<s1[i];
        }
        cout<<" "<<x<<endl;
    }
    return 0;
}