线段树

发表于 2023-01-05 更新于 2025-07-20 分类于程序设计竞赛

线段树

简介

二分创建 方法一数组线段树需要开4倍大小 方法二结构体数组 结构体数组开四倍大小更好：

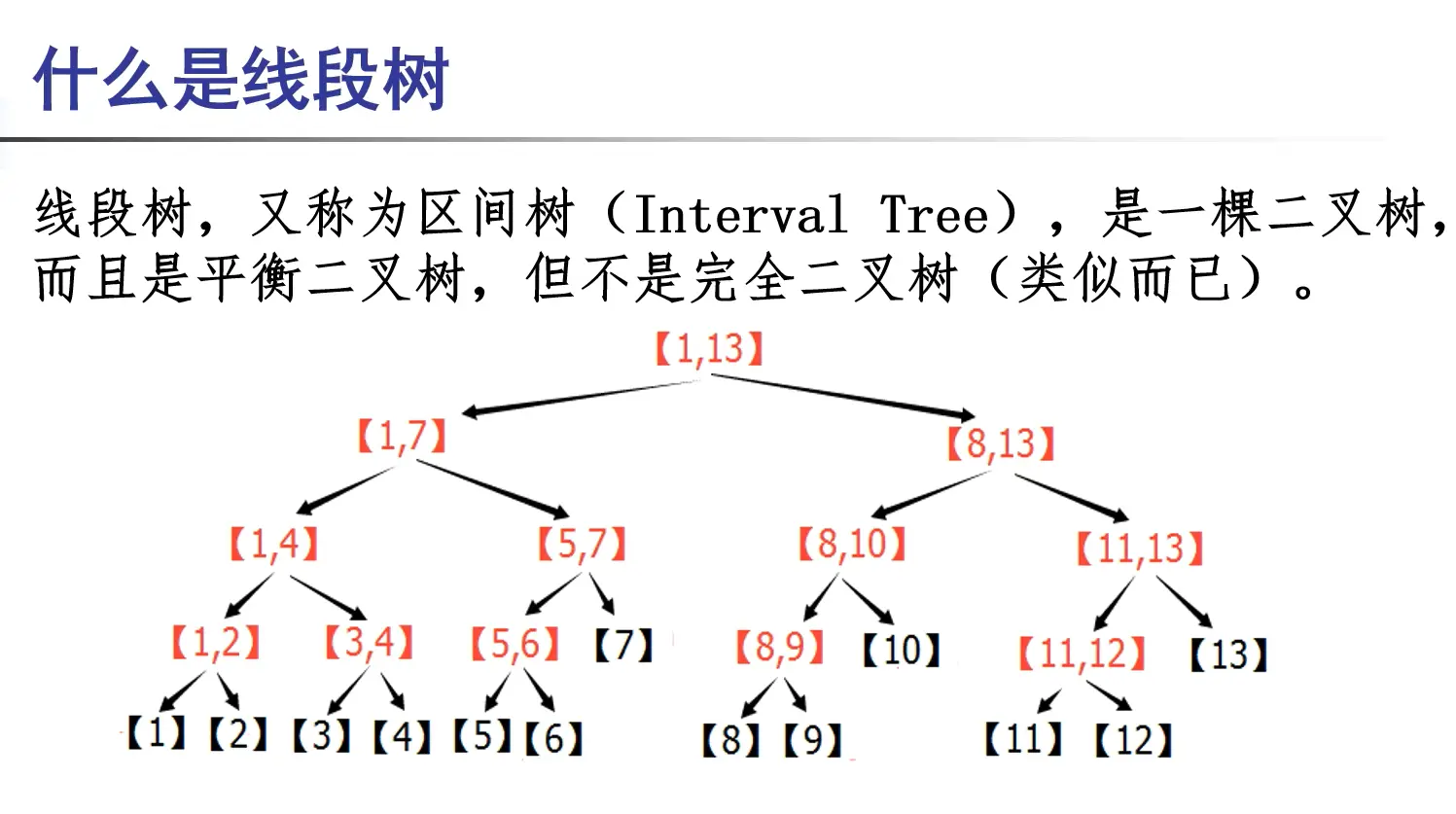
线段树的定义

#define maxn 100007 //元素总个数
int A[maxn]; //原始数组,不一定要用
struct SegTreeNode
{
    int val; //节点值，如区间最大值
    //int lazy; //懒惰标记，又称延迟更新标记
    //这里还可以根据题目需要增加更多的元素
} SegTree[maxn<<2]; //定义线段树

构造

使用到二叉树存储：

//PushUp函数更新节点信息，这里以求和为例
void PushUp(int rt)
{
    SegTree[rt].val = SegTree[rt<<1].val + SegTree[rt<<1|1].val;
}

void build(int l, int r, int rt)//构造根为rt,A区间为[l,r]线段树
{
    if(l == r)
    {
        //叶子节点
        SegTree[rt].val = A[l];
        return;
    }
    int m = (l + r) / 2;
    build(l, m, rt*2);//递归构造左子树
    build(m+1, r, rt*2+1);//递归构造右子树
    PushUp(rt);//回溯，向上更新
}

单点更新

从树根开始进行：单点更新(假设 A[L]+=C)

// l, r 表示当前节点区间，rt 表示当前线段树的根节点编号  
void Update(int L, int C, int l, int r, int rt) {  
    if (l == r) {  
        // 叶节点，直接修改  
        SegTree[rt].val += C;  
        return;  
    }  

    int m = (l + r) >> 1;  
    if (L <= m) Update(L, C, l, m, rt << 1);  
    else Update(L, C, m + 1, r, rt << 1 | 1);  
    PushUp(rt);  // 回溯，向上更新
}

区间查询

区间查询(询问A[L…R]的和)

// [L,R] 表示操作区间，[l,r] 表示当前区间，rt 表示当前节点编号
int Query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R)
        return SegTree[rt].val; // 在区间内直接返回
    if (L > r || R < l)
        return 0;

    int m = (l + r) >> 1;
    int ANS = 0;
    if (L <= m) ANS += Query(L, R, l, m, rt << 1); // 左子区间与[L,R]有重叠，递归
    if (R > m) ANS += Query(L, R, m+1, r, rt << 1 | 1); // 右子区间与[L,R]有重叠，递归
    return ANS;
}

区间更新

延迟标记

线段树的延迟标记

延迟标记：每个节点新增一个标记，记录这个节点是否进行了某种修改（这种修改操作会影响其子节点），对于任意区间的修改，我们先按照区间查询的方式将其划分成线段树中的节点，然后修改这些节点的信息，并给这些节点标记上代表这种修改操作的标记。

在修改和查询的时候，如果我们到了一个节点p，并且决定考虑其子节点，那么我们就要看节点p是否被标记，如果有，就要按照标记修改其子节点的信息，并且给予节点都标上相同的标记，同时消掉节点p的标记。

减少操作次数

操作代码

线段树的构造(有lazy标记)

//构造根为rt，A区间为[l,r]线段树
void build(int l, int r, int rt)
{
    //初始化延时标记为0
    SegTree[rt].lazy=0;
    if(l == r){
        //叶子节点
        SegTree[rt].val = A[l];
        return;
    }
    int m = (l + r) / 2;
    build(l, m, rt*2); //递归构造左子树
    build(m+1, r, rt*2+1); //递归构造右子树
    PushUp(rt); //回溯，向上更新
}

区间更新(以A[L,R]+=C为例)

void Update(int L, int R, int C, int l, int r, int rt) {
    if (L <= l && r <= R) {
        SegTree[rt].val += C * (r - l + 1);    // 更新数字和，向上保持正确
        SegTree[rt].lazy += C;                // 累加还是赋值，看需求
        return ;
    }
    int m = (l + r) >> 1;
    PushDown(rt, m - l + 1, r - m);            // 下推以后，才准确更新子节点
    if (L <= m) Update(L, R, C, l, m, rt << 1);
    if (R >  m) Update(L, R, C, m + 1, r, rt << 1 | 1);
    PushUp(rt);                                // 更新本节点信息
}

Pushdown 目的是将lazy标记传下去

//ln, rn 分别为左子树和右子树的区间大小
void PushDown(int rt,int ln,int rn){
    if(SegTree[rt].lazy){                      //下推标记
        SegTree[rt<<1].lazy += SegTree[rt].lazy;
        SegTree[rt<<1|1].lazy += SegTree[rt].lazy;
        SegTree[rt<<1].val += SegTree[rt].lazy * ln;
        SegTree[rt<<1|1].val += SegTree[rt].lazy * rn;

        SegTree[rt].lazy = 0;    //清除本节点标记
    }
}

区间查询

区间更新的区间查询（询问A[L…R]的和）

//[L,R]表示操作区间，[l,r]表示当前区间，rt表示当前区间根节点编号
int Query(int L, int R, int l, int r, int rt){
    if(L <= l && r <= R)
        return SegTree[rt].val;   //在区间内直接返回
    if(L > r || R < l)
        return 0;
    int m = (l + r) >> 1;
    PushDown(rt, m - l + 1, r - m);     //下推以后，才准确查询子节点
    return Query(L, R, l, m, rt << 1) + Query(L, R, m + 1, r, rt << 1 | 1);
}

例题一敌兵布阵

题目描述 Problem Description C国的死对头A国这段时间正在进行军事演习，所以C国间谍头子Derek和他手下Tidy又开始忙乎了。A国在海岸线沿直线布置了N个工兵营地,Derek和Tidy的任务就是要监视这些工兵营地的活动情况。由于采取了某种先进的监测手段，所以每个工兵营地的人数C国都掌握的一清二楚,每个工兵营地的人数都有可能发生变动，可能增加或减少若干人手,但这些都逃不过C国的监视。中央情报局要研究敌人究竟演习什么战术,所以Tidy要随时向Derek汇报某一段连续的工兵营地一共有多少人,例如Derek问:“Tidy,马上汇报第3个营地到第10个营地共有多少人!”Tidy就要马上开始计算这一段的总人数并汇报。但敌兵营地的人数经常变动，而Derek每次询问的段都不一样，所以Tidy不得不每次都一个一个营地的去数，很快就精疲力尽了，Derek对Tidy的计算速度越来越不满:”你个死肥仔，算得这么慢，我炒你鱿鱼!”Tidy想：“你自己来算算看，这可真是一项累人的工作!我恨不得你炒我鱿鱼呢!”无奈之下，Tidy只好打电话向计算机专家Windbreaker求救,Windbreaker说：“死肥仔，叫你平时做多点acm题和看多点算法书，现在尝到苦果了吧!”Tidy说：”我知错了。。。”但Windbreaker已经挂掉电话了。

Tidy很苦恼，这么算他真的会崩溃的，聪明的读者，你能写个程序帮他完成这项工作吗？不过如果你的程序效率不够高的话，Tidy还是会受到Derek的责骂的.

Input 第一行一个整数T，表示有T组数据。每组数据第一行一个正整数N（N<=50000）,表示敌人有N个工兵营地，接下来有N个正整数,第i个正整数ai代表第i个工兵营地里开始时有ai个人（1<=ai<=50）。接下来每行有一条命令，命令有4种形式： (1) Add i j,i和j为正整数,表示第i个营地增加j个人（j不超过30） (2)Sub i j ,i和j为正整数,表示第i个营地减少j个人（j不超过30）; (3)Query i j ,i和j为正整数,i<=j，表示询问第i到第j个营地的总人数; (4)End 表示结束，这条命令在每组数据最后出现; 每组数据最多有40000条命令

Output 对第i组数据,首先输出“Case i:”和回车, 对于每个Query询问，输出一个整数并回车,表示询问的段中的总人数,这个数保持在int以内。

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
#define ll long long

int n;
int c[100000];

int lowbit(int x){
    return x & -x;
}

void update(int i,int val){
    while(i<=n){
        c[i]+=val;
        i+=lowbit(i);
    }
}

int sum(int i){
    int num=0;
    while(i>0){
        num+=c[i];
        i-=lowbit(i);
    }
    return num;
}

int calc(int a,int b){
    return sum(b)-sum(a-1);
}

int main(){
    int t;
    cin>>t;
    int cnt=1;
    while(cnt<=t){
        printf("Case %d:\n",cnt);
        memset(c,0,sizeof(c));
        scanf("%d",&n);
        for(int i=1;i<=n;i++){
            int temp;
            scanf("%d",&temp);
            update(i,temp);
        }
        char ss[10];
        scanf("%s",ss);
        while(ss[0]!='E'){
            int a,b;
            scanf("%d%d",&a,&b);
            if(ss[0]=='Q'){
                printf("%d\n",calc(a,b));
            }
            else if(ss[0]=='A'){
                update(a,b);
            }
            else if(ss[0]=='S'){
                update(a,-b);
            }
            scanf("%s",ss);
        }
        cnt++;
    }

    return 0;
}

例题二

杭电ACM-LCY算法培训-例2

题目大意：

给定n个整数和m个操作，输出查询结果，操作有2类（如下）：

U A B：将第A个元素替换为B（索引从0开始计数）
Q A B：输出[a,b]中最长的连续递增子序列（LCIS）的长度。

10 3 7 7 3 3 5 9 9 8 1 8 Q 6 6 U 3 4 Q 0 1

解题思路

题目分析：对于任意一个节点：max则是综合当前节点的整个区间得到的LCIS。 lmax存的是从当前节点的最左端开始的LCIS；rmax存的是从当前节点的最右端开始的LCIS。

左儿子最右边的值 >= 右儿子最左边的值 max = MAX(左儿子的max，右儿子的max)；
左儿子最右边的值 < 右儿子最左边的值对应 a[mid] < a[mid + 1] lmax = (左儿子的lmax==左儿子的区间长度len)?左儿子的len+右儿子的lmax:左儿子的lmax ； rmax = (右儿子的rmax==右儿子的区间长度len)?右儿子的len+左儿子的rmax:右儿子的rmax ； max = MAX(左儿子的max，右儿子的max，左儿子的rmax + 右儿子的lmax)；

思考：如何定义线段树节点的结构体？

总结：本题考查知识点——线段树 + 区间合并

总结

线段树的应用范围

用线段树统计的东西，必须符合区间”加法”！否则，不可通过二分子区间来得到[L,R]的统计结果。

符合区间加法的常见例子：

区间数字之和 = 左区间数字之和 + 右区间数字之和
区间最大值 = max(左区间最大值, 右区间最大值)
区间最大公因数(GCD) = gcd(左区间GCD, 右区间GCD)

线段树重要！重要！重要！ 一个问题只要能转化成对一些连续点的修改和统计问题，基本就可以用线段树来解决！今天只是线段树入门，能走多远修行在个人～

线段树

简介

构造

单点更新

区间查询

区间更新

延迟标记

操作代码

例题一 敌兵布阵

例题二

杭电ACM-LCY算法培训-例2

题目大意：

总结

例题一敌兵布阵