拓补排序+邻接表

发表于 更新于 分类于

拓补排序+邻接表

拓补排序定义

需要在有向无环图中

所谓“拓扑排序”，是指将一个有向无环图G的所有顶点排成一个线性序列，使得有向无环图G的边集中的任意一条边<u, v>，始终满足u出现在v的前面。

通常，这样的序列称为是“拓扑序列”。

拓扑排序算法基本思想

  1. 在有向无环图中找到一个没有前驱的节点（或者说是入度为0的节点）输出；
  2. 然后从图中将此节点删除并且删除以该节点为尾的弧；
  3. 如果所有节点都已输出，则程序结束；否则，返回步骤1；

例题1

题目描述：

有N个队参加比赛（1<=N<=500），队伍编号依次为1, 2, 3, …, N，比赛结束后，裁判委员会要将所有参赛队伍依次排名，但现在裁判委员会只知道每场比赛的结果，比如P1赢P2，用P1 P2表示，则排名时P1应该在P2之前。现在，请你编程确定最终的全部排名。排名若不唯一，则编号小的队伍在前。

Input 4 3 1 2 2 3 4 3

Output 1 2 4 3

如果加上BFS使用队列处理入队列0入度点

解题代码：

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
#define ll long long

int cnt;
int n,m;
int head[510];
int inn[510];
struct node {
    int to;
    int next;
}edge[200005];

void add_edge(int from,int to){
    edge[++cnt].to=to;
    edge[cnt].next=head[from];
    head[from]=cnt;
    inn[to]++;
    return ;
}

int findzero(){
    for(int i=1;i<=n;i++){
        if(inn[i]==0){
            inn[i]--;
            return i;
        }
    }
    return 0;
}

int main(){
    while(cin>>n>>m){
        for(int i=0;i<=n;i++){
            inn[i]=0;
            head[i]=-1;
        }
        cnt=0;
        for(int i=1;i<=m;i++){
            int from,to;
            scanf("%d%d",&from,&to);
            add_edge(from,to);
        }
        int num=0;
        while(int cur=findzero()){
            num++;
            if(num==n){
                cout<<cur<<endl;
                break;
            }
            cout<<cur<<" ";
            for(int k=head[cur];~k;k=edge[k].next){
                inn[edge[k].to]--;
            }
        }
    }
    return 0;
}

例题二

题目描述：

临近春节，甘老板决定为每个员工发红包。 现在的问题是，每人发多少红包呢？要知道，很多员工提出了自己的要求，比如，胡承轩就提出他的红包应该比麻致远的大！

为了图吉利，甘老板决定为每名员工至少发888的红包，同时，他还希望能满足员工们提出的所有的要求，当然，最后是希望发出红包的总金额最少。

员工数：n<=10000 提出的要求：m<=20000

Input 

2 1
1 2
2 2
1 2
2 1

Output 

1777 -1

可以反向建图+DP思想（money）

解题代码：

#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define ll long long

int n,m;
int cnt;
int head[10010];
int inn[10010];
int money[10010];
struct node{
    int to;
    int next;
}edge[20010];

void add_edge(int from,int to){
    edge[++cnt].to=to;
    edge[cnt].next=head[from];
    inn[to]++;
    head[from]=cnt;
    return ;
}

int findzero(){
    for(int i=1;i<=n;i++){
        if(inn[i]==0){
            inn[i]--;
            return i;
        }
    }
    return 0;
}

int main(){
    while(cin>>n>>m){
        for(int i=0;i<=n;i++){
            head[i]=-1;
            inn[i]=0;
            money[i]=888;
        }
        cnt=0;
        for(int i=1;i<=m;i++){
            int from,to;
            scanf("%d%d",&to,&from);
            add_edge(from,to);
        }
        ll ans=0;
        int num=0;
        while(int cur=findzero()){
            num++;
            ans+=money[cur];
            for(int k=head[cur];~k;k=edge[k].next){
                int to=edge[k].to;
                inn[to]--;
                money[to]=max(money[to],money[cur]+1);
            }
        }
        if(num!=n){
            cout<<"-1"<<endl;
            continue;
        }
        cout<<ans<<endl;
    }

    return 0;
}

邻接表存储表

回顾：STL中vector的经典应用-邻接表

struct edge{
    int from, to, value;
} //定义边

const int maxn = 10005;

vector<edge> Map[maxn]; //一维向量相当于二维数组

若用普通二维数组存邻接表，则需要1e8的空间开销，而图中实际边数只有20000，则无疑会造成极大浪费（易超内存）。

//初始化，clear函数是清空向量，不是变成0。
for(int i=0; i<maxn; i++)
    Map[i].clear();

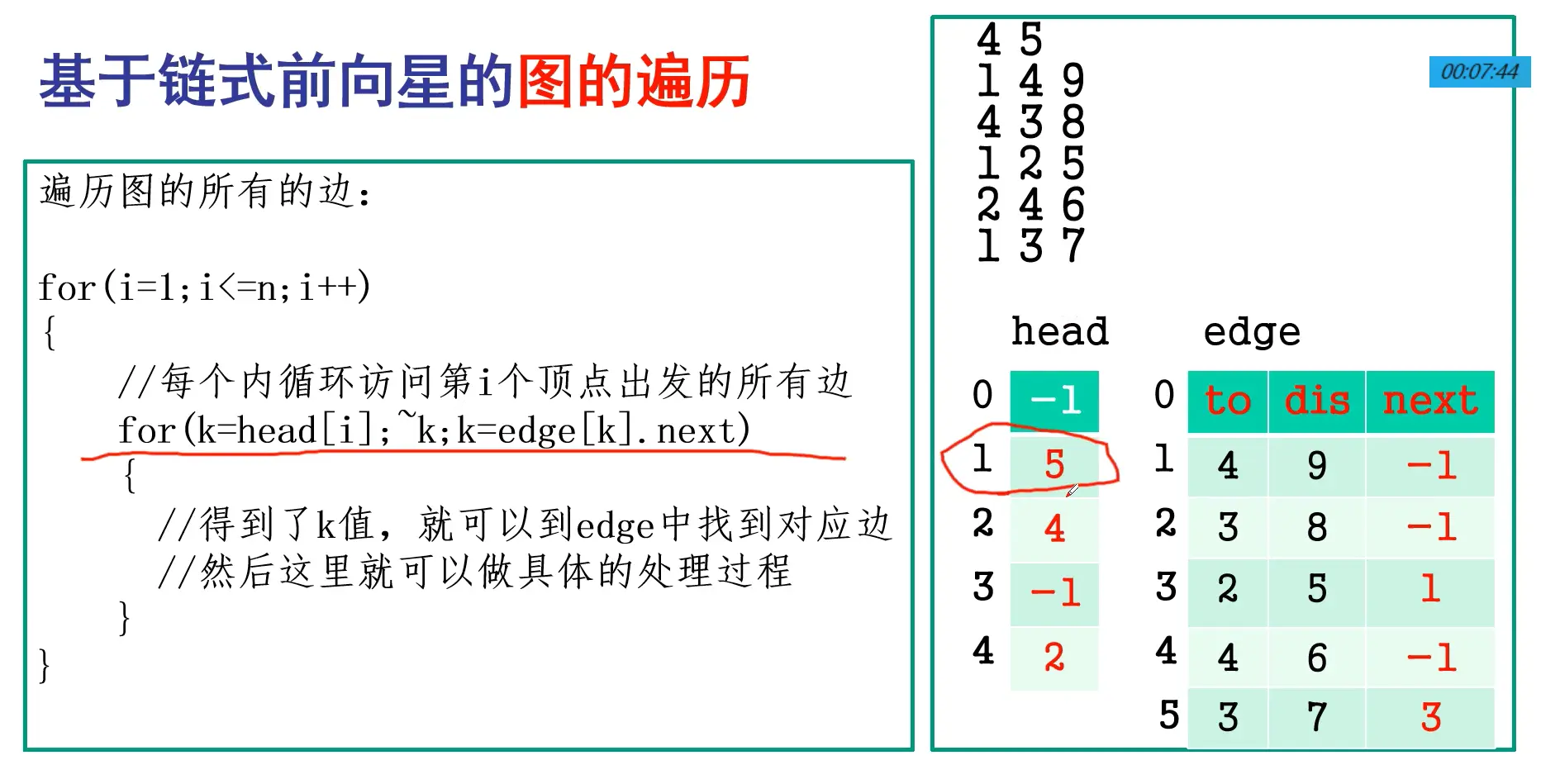
链式前向星（邻接表数组实现）